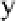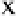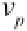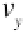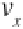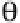Game Development Reference
In-Depth Information
and concepts developed in the previous section can be applied to a general two-body collision.
In this section, the equations will be developed to model two-dimensional collisions.
•
The collision will affect the velocity components along (that is, parallel to) the line of
action of the collision.
•
Velocity components perpendicular to the line of action are unchanged by the collision.
The key to general two-dimensional collision analysis is to rotate the frame of reference so
that one axis of the rotated coordinate system is parallel to the line of action for the collision.
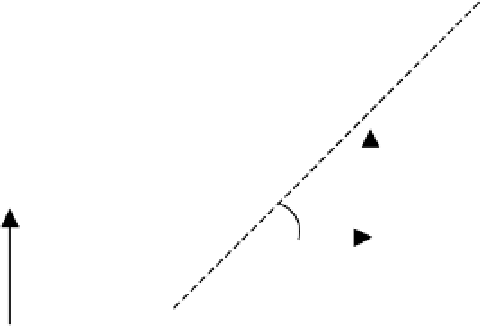
A two-dimensional collision, as the name would suggest, is one where the vector that defines
the line of action lies in a two-dimensional plane. For example, consider the collision between
object 1 and object 2 shown in Figure 6-6. The collision takes place in the x-y plane, and the line
of action of the collision is at an angle
q
with respect to the x-axis.
Figure 6-6.
A general two-dimensional collision
Object 1 has pre-collision velocity components in the x- and y-directions equal to
v
x
and
v
y
. In order to analyze the collision, the velocity along the line of action,
v
p
, must be determined.
Once
v
p
has been calculated, the post collision velocities along the line of action can be calcu-
lated according to Equation (6.14a). The velocity along the line of action can be computed from
the trigonometric relation shown in Equation (6.16).
v
p
=
v
x
cos
θ
+
v
y
sin
θ
(6.16)
Let's dig a little deeper into where Equation (6.16) came from. To get the velocity along the
line of action, the original Cartesian coordinate system has to be rotated by an angle of
q
as
shown in Figure 6-7.