Java Reference
In-Depth Information
cos
0
sin
(
i
+
1)
( )
i T
−
1
M
=
(
M
)
0
1
0
−
sin
0
cos
and
1
0
0
,
(
i
+
1)
( )
i T
−
1
M
=
(
M
)
0
cos
−
sin
0
sin
cos
M
(
i
)
where and are the increases in angles for turning left and pitching up, and
is the
directional cosine matrix in the
i
ith rotation.
In the example code segment shown from Figures 4 to 7, the previous equation is used
in lines 12 to 35 to form and return a transformation matrix for the purpose of rotation
about one of the two possible axes x and y. In lines 36 to 46, the rotation operation is
carried out in a function whose first argument corresponds to the target transform group
that needs to be worked on. For this navigation example, the target transform group is of
course the one for the ViewPlatform. The second argument of the function is the angle to
be used in the rotation, and this may be equal to either or depending on the value of
the third argument. The latter is an integer mode argument with 1 denoting left rotation
and 2 denoting up pitching.
In the same manner, the mathematical formula for translation is given by
x
= + ∆
x
sin
cos
i
+
1
i
z
= + ∆
z
,
i
+
1
i
x
= + ∆
x
sin
+
i
+
1
i
2
z
= + ∆
z
cos
+
i
+
1
i
2
and
y
+
= + ∆
y
i
1
i
for implementing forward, left and up movements, respectively. Note that
x
i
,
y
i
and
z
i
are
the x, y and z coordinates of the viewpoint, and
∆
is the movement increment. Lines 48
to 55 of Figure 5 give the code for the function for translation.


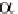
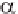



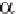
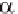



Search WWH ::

Custom Search