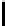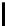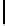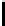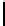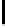Cryptography Reference
In-Depth Information
Tabl e 3.
Cost estimate for various optimal (
p,
) the first (top) table corresponds to
encryption, the second to digital signature and the third to hashing
(
n, r, w
) = (4096
,
540
,
45)
p
6 7 8 9 10 11
12
13 14 15 16 17
34 38 43 47 51 56
60
64 68 72 76 80
log
2
T
(
p,
) 129
.
4 129
.
0 128
.
7 128
.
5 128
.
4 128
.
3
128
.
3
128
.
4 128
.
6 128
.
9 129
.
2 129
.
6
(
n, r,w
)=(2
20
,
180
,
11)
p
4 5 6 7 8 9
10
41 50 59 68 77 86
94
log
2
T
(
p,
) 106
.
1 102
.
1 98
.
2 94
.
6 91
.
2 88
.
1
87
.
7
(
n, r, w
)=(2
21
,
1024
,
256)
p
11 12 13 14 15
16
17 18 19 20 21 22
103 112 121 129 138
144
145 146 147 148 148 149
log
2
T
(
p,
) 158
.
4 155
.
1 151
.
8 148
.
5 145
.
3
144
.
0
144
.
9 145
.
8 146
.
7 147
.
7 148
.
6 149
.
5
We keep the same notations and use the same assumptions and approxima-
tionsasin
§
4. We denote
− ε
(
p,
))
N|W
1
||W
2
|
≈
P
N
(
p,
)=1
−
(1
min (1
,ε
(
p,
)
N|W
1
||W
2
|
)
the probability for one execution of doom loop to succeed. We have a statement
very similar to Proposition 1.
Proposition 2.
For an input
(
H
0
,S
0
)
such that
CSD(
H
o
,s
0
,w
)
=
∅
for all
s
0
∈S
0
the Algorithm 4 will stop after executing
P
N
(
p,
)
+
K
1
|W
1
|
K
0
K
2
|W
1
|ε
(
p,
)
+
K
3
2
ε
(
p,
)
≈T
N
(
p,
)=
P
N
(
p,
)
+
(9)
elementary operations on average.
We omit the proof which is similar to the proof of Proposition 1 with an identical
expression for the complexity except for
P
N
(
p,
) (which grows with
N
).
5.1 Cost of Linear Algebra
The constant
K
0
will include, in addition to the Gaussian elimination, the com-
putation of all the
s
o
U
T
for
s
0
∈S
0
. This multiplies the cost, at most, by a
factor
N
=
(with larger
N
just reading the instances would be the bottleneck, so we discard that possi-
bility) the probability
1
/ε
(
p,
)
k
+
p
|S
0
|
. On the other hand, as long as
N ≤
P
N
(
p,
)is
N
times larger than before and thus the ratio
K
0
/P
N
(
p,
) do not increase. The total cost
(
p,
), so
the relative contribution of the linear algebra will increase, but the simplification
K
0
= 0 remains reasonable as long as
T
N
(
p,
) is smaller than
T
P
N
(
p,
)
1.
When
N
is close or equal to 1
/ε
(
p,
)
k
+
p
,asin
5.3, the situation is not
so simple. With fast binary linear algebra computing all the
s
o
U
T
will require
§