Biomedical Engineering Reference
In-Depth Information
FIGURE 9.9
Y
General isentropic flow in an expand-
ing channel. In general, we would be interested in the
temperature, pressure, density, and velocity of the fluid
for a given change in area. The fluid mechanics govern-
ing equations for compressible flows can be found in
the following discussion.
X
R
x
Flow
Location 1
T
1
,
p
1
,
1
,
A
1
,
v
1
Location 2
T
2
,
p
2
,
2
,
A
2
,
v
2
Similarly, the first and second law of thermodynamics can be written as
v
1
v
2
2
5
h
2
2
5
h
0
h
1
1
1
ð
9
:
14
Þ
s
1
5
s
2
5
s
ð
9
:
15
Þ
where h
5
u
1
pV and h
0
is defined as the stagnation enthalpy. The stagnation enthalpy is
the enthalpy that would be obtained if the fluid were decelerated to a zero velocity. For
many compressible fluids, the enthalpy and the density are tabulated as functions of
entropy and pressure. If the fluid is an ideal gas (or if it is valid to assume that it is an
ideal gas) then the following equations can be used during problem solving:
p
5
ρ
RT
ð
9
:
16
Þ
h
2
2
h
1
5
c
p
ð
T
2
2
T
1
Þ
ð
9
:
17
Þ
p
ρ
k
5
constant
ð
9
:
18
Þ
where k is the ratio of specific heats k
5
c
p
=
c
v
.
The Mach number (M) is defined as the ratio of the fluid velocity to the speed of sound:
v
c
M
5
ð
9
:
19
Þ
For most, if not all, biological applications, flow will be subsonic in which the Mach num-
ber is less than 1. In this case, a decrease in cross-sectional area causes an increase in veloc-
ity, while an increase in cross-sectional area causes a decrease in flow velocity. However,
in supersonic flows (M
.
1), the effects are exactly opposite. Flow accelerates in an
expanding channel and decelerates in a narrowing channel.
Let us now consider the compressible flow through a channel with friction but no heat
transfer. This assumption is valid if the channel is relatively short. For these conditions all of
the previous equations remain the same except for
Equations 9.13 and 9.15
.In
Equation 9.13
,






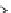










Search WWH ::

Custom Search