Cryptography Reference
In-Depth Information
G
. Wir setzen
G
(A2) Es seien
G
=
c
+
F
b
∈G
und
a
∈A\
:
=
a
+
F
b
. Wegen
a
∈
G
sind die Nebenklassen
G
und
G
F
des Untervektorraums
b
disjunkt, folglich
G
= ∅
gilt
G
∩
.
Ist nun
G
eine weitere Gerade mit
G
∩
= ∅
G
durch
a
, so können wir
G
=
a
+
F
d
mit einem
d
=
0 setzen. Die Gleichung
a
+
λ
d
=
c
+
μ
b
hat dann
2
. Daher können die Vektoren
b
,
d
2
(
λ
μ
)
∈
F
∈
F
keine Lösung
,
nicht linear un-
=
F
d
und damit
G
=
G
.
abhängig sein. Es folgt
F
b
=(
)
=(
)
=(
)
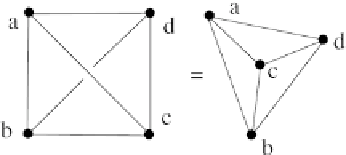
(A3) Die drei Punkte
a
:
0, 0
,
b
:
1, 0
,
c
:
0, 1
erfüllen die gewünsch
te
Bedingung.
Es heißt
(
F
)
=(
A
G
)
AG
2,
:
,
(
F
)
die
affine Ebene
über
die wichtigste Klasse von Beispielen für
affinen Ebene. Wir geben ein weiteres interessantes Beispiel.
F
. Es ist AG
2,
Beispiel
Es ist
A
=
{
}
G
=
{{
}
{
}
{
}
{
}
{
}
{
}}
a
,
b
,
c
,
d
mit
a
,
b
,
a
,
c
,
a
,
d
,
b
,
c
,
b
,
d
,
c
,
d
eine affine Ebene, genannt das
Minimalmodell
einer affinen Ebene. Es ist die
affine Ebene mit der geringsten An-
zahl von Punkten. Nach Aufgabe 5.2
hat nämlich jede affine Ebene mindes-
tens vier Punkte. Die Geraden sind die
zweielementigen Teilmengen von
A
.
5.3.3 Netze
G⊆
(
)
|
≥
∈G
(
G
)
Es sei
K
eine Menge und
Pot
K
mit
|
G
2 für alle
G
. Das Paar
K
,
heißt
Netz
, wenn gilt:
(A1)' Zu
a
,
b
∈
=
∈G
∈
K
,
a
b
, gi
bt e
s höchstens ein
G
mit
a
,
b
G
; im Fall der
Existenz schreiben wir
a
,
b
für dieses
G
.
(A2) (
Parallelenaxiom
)Zu
G
∈G
und
a
∈
K
\
G
existiert genau eine Gerade
G
∈G
G
und
G
G
= ∅
mit
a
∈
∩
.
(A3)' Es gibt mindestens drei Geraden, die paarweise Schnittpunkte besitzen.
Weil aus (A3) leicht (A3)' folgt, ist klar, dass jede affine Ebene ein Netz ist.
Zwei Geraden
G
,
H
eines Netzes heißen
parallel
, wenn
G
=
∩
= ∅
H
oder
G
H
.
∈
Für die zur Geraden
G
durch den Punkt
a
K
eindeutig bestimmte Parallele
schreiben wir
{
a
G
}
. Es gilt also
a
∈{
a
G
}
G
. Ein Netz
(
K
,
G
)
heißt
|
|∈
N
endlich
, falls
K
.
Lemma 5.4
Es sei
(
K
,
G
)
ein endliches Netz, dann gilt: