Biomedical Engineering Reference
In-Depth Information
Low energy
High energy
10
3
10
2
10
-2
10
-3
10
1
0.1
Wavelength (m)
10
5
10
6
10
7
10
8
10
9
10
10
10
11
10
12
10
13
10
14
10
15
10
16
10
17
10
18
10
19
Frequency (Hz)
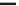
FIGURE 4.1
The electromagnetic spectrum.
The electric field flux Φ
e
through a surface is given by
In the case of the magnetic field, moving charges need to be
considered. The magnetic flux density
B
is defined through
=
∫
EdS
Φ
e
.
(4.5)
(
)
F
=
q
v
×
B
(4 .11)
m
q
S
where
dS
is an elemental surface area and
dS
is the vector of
magnitude
dS
directed along the outward normal to the elemen-
tal area. For a single charge, from Equation 4.1, the right-hand
side of Equation 4.5 can be written
where
v
q
is the velocity of charge
q
. The vector product in
Equation 4.11 shows that the force
F
m
is normal to both
v
and
B
.
The total magnetic flux density
B
P
at a point
P
due to a com-
plete current circuit is given by
1
q
r
1
∫
∫
∫
EdS
.
=
r dS
.
=
d
Ω
(4.6)
=
µ
π
dl
×
r
∫
2
4
πε
4
πε
0
l
(4.12)
B
I
P
2
4
r
S
S
S
l
where
d
Ω is the solid angle subtended at
q
by
dS
. Since the inte-
gral of the solid angle over a closed surface is 4π:
where μ
0
is the permeability of free space (= 4π × 10
−7
H m
−1
),
I
is
the current in the circuit,
dl
is an elemental length of wire,
r
is the
distance between
dl
, and point
P
and
r
is the unit vector directed
from
dl
to
P
. This relationship is known as the Biot-Savart law.
q
∫
EdS
.
=
ε
(4.7)
S
and when the charge can be represented by a continuous charge
density ρ(
r
):
4.3 time-Varying Electric
and Magnetic Fields
1
∫
∫
EdS
.
=
ε
ρ
dV
.
(4.8)
Time-varying electric and magnetic fields are described by the
set of equations known as Maxwell's equations. In integral form,
the equations describing fields in free space are
S
V
The total electric field flux passing out through a closed surface
is equal to the total charge within the surface divided by ε. This
is the integral form of Gauss's law. Using Equation 4.7 and the
divergence theorem:
1
∫
∫
EdS
.
=
ε
ρ
dV
(4.13a)
S
V
∫
=
∫
EdS
.
.
E
dV
(4.9)
=−
∂
∂
B
∫
∫
(4.13b)
Edl
.
.
dS
t
S
V
l
S
Equation 4.8 may be rewritten as
∫
BdS
.
=
0
(4.13c)
⋅−
ρ
ε
⋅=
ρ
∫
E
dV
=
0
or
ε
(4.10)
S
V
∂
∂
E
∫
∫
∫
Bdl
.
=µ
J dS
.
+ε µ
.
dS
(4.13d)
0
0
0
t
which is the differential form of the Gauss law and states that
the electric field flux out per unit volume from a point is propor-
tional to the charge density at that point.
l
S
S
where
J
is the current density (A m
−2
).