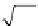Biomedical Engineering Reference
In-Depth Information
process within a solid immersed in a fluid environment. The
solution for the internal temperature field is
where
Fo
is called the Fourier number, representing a dimen-
sionless time. It is the ratio of the actual process time compared
to the thermal diffusion time constant for the system.
The Fourier equation (Equation 1.11) in one dimension can be
written in terms of these dimensionless variables as
2
TxtT
TT
(,)
−
x
hx
k
ht
k
α
−
s
=
erfc
exp
+
2
−
2
α
t
i
s
x
ht
kw
α
∗
2
∗
∂θ
∂
=
∂θ
∂
(1.14)
×
erfc
+
(1.19)
2
α
t
∗
2
Fo
x
where
erfc
φ is the complementary error function defined as
erfc
φ
= 1 −
erf
φ.
for which the initial and boundary conditions are written as
∗∗
θ
x
(,0)
=
1
(1. 20)
1.2.2.3 Semi-Infinite Geometry—Defined
Surface Heat Flux:
∂
Tt
t
(0,)
Q
A
s
−
k
==
q
∗
∗
∂θ
∂
s
∂
(1. 21)
=
0
x
A heat flow per unit area of the surface is assumed to be applied
instantaneously and then maintained continuously for the dura-
tion of the process. Typical causes of this boundary condition
are an external noncontact energy source that is in communi-
cation with the surface of a solid via electromagnetic radiation.
The solution of this problem is
∗
x
=
0
which is a result of thermal and geometric symmetry,
=θ
∗
∗
−
∂θ
∂
∗
(
)
Bi
1,
Fo
(1. 22)
x
∗
x
=
1
2
−
2
q
−
x
qx
k
x
α
π
t
where
Bi
is defined as the Biot number, which represents the
ratio of thermal resistances by condition on the interior of the
solid and by convection at the surface interface with a fluid
environment:
s
s
TxtT
(,)
−=
exp
erfc
(1.15)
i
k
4
α
t
2
α
t
1.2.2.4 Finite Dimensioned System with
Geometric and thermal Symmetry
Another boundary condition encountered frequently occurs
when a finite-sized solid is exposed to a new convective envi-
ronment in a stepwise manner. If the system and process both
exhibit geometric and thermal symmetry, an explicit mathemat-
ical solution exists for one-dimensional Cartesian, cylindrical,
and spherical coordinates in the form of an infinite series. As
will become apparent, it is advantageous to write the problem
statement and solution in terms of dimensionless variables.
The temperature is scaled to the environmental value as
θ= −
∞
hL
k
L
kA
hA
Bi
==
.
(1. 23)
1
The solution for this problem is in the form of an infinite
series,
∞
∑
(
)
2
∗
−ζ
Fo
∗
θ=
Ce
cos
ζ
x
(1. 24)
n
n
n
=
1
TT
and is normalized to the initial value:
where
C
n
satisfies for each value of
n
,
θ=
θ
θ
TT
TT
.
−
−
∗
∞
∞
=
(1.16)
4sin
2sin(2
ζ
ζ+ ζ
i
i
n
C
=
(1. 25)
n
)
n
n
Likewise, the independent variables for position and time are
normalized to the size and thermal time constant of the system,
and the eigenvalues
ζ
n
are defined as the positive roots of the
transcendental equation
x
L
∗
x
=
(1.17)
ζζ=
tan
Bi
.
(1. 26)
n
n
where
L
is the half width of the system along the primary ther-
mal diffusion vector,
Thus, there are unique values of
C
n
and
ζ
n
for each value of
Bi
.
The first six roots of this expression have been compiled as a
function of discrete values for
Bi
between 0 and ∞, and are avail-
able widely (Carslaw and Jaeger 1959).
==
α
t
L
2
∗
(1.18)
t
o