Biomedical Engineering Reference
In-Depth Information
This expression is known as
Fourier's equation
, and it has units
of W/m
3
. Although Equation 1.9 was derived in Cartesian
coordinates, it can be generalized to be applicable for alternate
coordinate systems:
system may be described in terms of a defined temperature, heat
flux, or convective process. The energy source applied to create a
hyperthermia state in tissue nearly always results in a geometri-
cally complex internal temperature field imposed onto the system
of analysis. The source can be viewed as a type of internal bound-
ary condition. The solution of the Fourier equation issues in an
understanding of the spatial and temporal variations in tempera-
ture,
T
(
x,y,z,t
), which can then be applied to predict the therapeu-
tic outcome of a procedure. This analysis is covered in Chapter
2, this topic. he solution for the temperature ield in tissue may
also be incorporated into feedback control algorithms to achieve
specific therapeutic outcomes.
Several classes of boundary conditions will be discussed to
illustrate how different environmental interactions influence
the flavor of the solution for the temperature field. We will first
consider semi-infinite geometries for which there is an exposed
surface of the tissue and an elevated temperature develops over
space and time in the interior. The overall tissue dimensions are
assumed to be large enough so that the effects of the free sur-
face on the opposing side of the body are not encountered. This
geometry simplifies to a one-dimensional Cartesian coordinate
system, which we will represent in the coordinate
x
. he three
classes of boundary conditions we will consider for semi-infinite
geometry are: (a) constant temperature, (b) convection, and (c)
specified heat flux.
∂
∂
T
t
(
)
ρ
c
=
kT
.
(1.10)
p
The foregoing equation may be divided by the product ρ
c
p
to iso-
late the temperature term on the left side. The resulting thermal
property is the thermal diffusivity, α =
k
/ρ
c
:
∂
∂
=α
T
t
(
)
T
.
(1.11)
Applications involving therapeutic hyperthermia generally
involve the deposition of a temporally and spatially distributed
internal energy source to elevate the temperature within a target
tissue. In this case, the energy generation term must be included
in the conservation of energy equation, resulting in
Q
∂
∂
=α +
ρ
T
t
gen
(
T
)
.
(1.12)
c
p
1.2.2.1 Semi-Infinite Geometry—Constant
Surface temperature:
TtT
The complete solution of Equation 1.11 requires the specifica-
tion of one (initial) boundary condition in time and two spa-
tial boundary conditions for each coordinate dimension along
which the temperature may vary independently. These bound-
ary conditions are used to evaluate the constants of integration
that result from solution of the partial differential equation.
They are determined according to: (a) the geometric shape of
the system, including whether there is a composite structure
with component volumes having distinct material properties;
(b) what the temperature field interior to the system is like at
the beginning of the process; (c) the geometry of imposed heat
transfer interactions with the environment, such as radiation
and/or convection; and (d) how these environmental interac-
tions may change over time. As an aggregate, these four types
of conditions dictate the form and complexity of the math-
ematical solution to Equation 1.11, and there are many differ-
ent outcomes that may be encountered. Mathematical methods
for solving this equation have been available for many decades,
and some of the most comprehensive and still useful texts are
true classics in the field (Morse and Feshback 1953; Carslaw and
Jaeger 1959).
The temporal boundary condition is generally defined in
terms of a known temperature distribution within the system at
a specific time, usually at the beginning of a process of interest.
However, definition of the spatial boundary conditions is not so
straightforward. There are three primary classes of spatial bound-
ary conditions that are encountered most frequently. The thermal
interaction with the environment at the physical boundary of the
(0,)
=
A temperature
T
s
is assumed to be applied instantaneously to the
surface of a solid and then to be held constant for the duration of
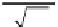
the process. The solution for this problem is the Gaussian error
function,
erf
φ, where
∫
2
2
erf
=
exp(
−ξ
).
d
ξ
π
For a uniform initial temperature,
T
i
, throughout the mate-
rial, the solution is expressed as a dimensionless ratio as
TxtT
TT
(,)
−
x
s
=
erf
.
(1.13)
−
2
α
t
i
s
1.2.2.2 Semi-Infinite Geometry—Convection:
k
∂
Tt
t
(0,)
−
=
hT
[
−
Tt
(0, )]
∞
∂
Here, the symbol
h
is the convective heat transfer coefficient (in
other contexts it may be used for specific enthalpy (Equation 1.1)
or for the Planck constant (Equation 1.71)), which is a function
of the boundary interaction between a solid substrate and the
environmental fluid that is at a temperature
T
∞
. Convective heat
transfer analysis is focused primarily on determining the value
for
h
to be applied as the boundary condition for a conduction