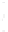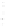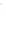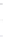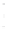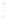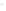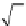Biomedical Engineering Reference
In-Depth Information
a normalized error less than or equal to 1% throughout the
entire grid is
N
= 176. The computational grid extends out to
a
2
/λ in the axial direction (which is equal to the far-field transi-
tion distance defined in Equation 6.6 with
d
= 2
a
), and the lateral
grid boundary is located at
x
= ±1.5
a
. Numerical calculations
of the Rayleigh-Sommerfeld integral for this square piston are
evaluated on the same desktop computer described previously
for near-field pressure simulations with a circular piston. The
computation time for a 121-point by 101-point grid with
N
= 176
is 168.74 seconds (just under 3 minutes).
2
1
0
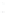
6.2.1.3 Spherical Shell
The spherically focused piston or spherical shell, which enhances
the peak intensity generated by a single ultrasound transducer
through geometrical focusing, is an ideal transducer shape
for thermal therapy. An example of a spherical shell with radius
a
and radius of curvature
R
= 2
is shown in Figure 6.5. The
mathematical description of this curved transducer geometry is
obtained when a plane slices through a sphere with radius
R
. he
intersection of the sphere and the plane describes a circle with
radius
a
, and the smaller of the two pieces is the spherical cap
or spherical shell. For a spherically focused source with uniform
normal particle velocity
U
0
, aperture radius
a
, and radius of cur-
vature
R
, the Rayleigh-Sommerfeld integral for a time-harmonic
excitation is given by
−1
−2
−2
−1
0
1
2
x
(units of piston half-width
a
)
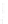
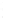
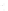
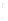
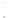
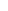
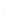
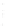
FIGURE 6.3
Square 2
a
by 2
a
piston centered in the
z
= 0 plane at
(
x ,y,z
) = (0,0,0). The normal at the center of the square piston is coinci-
dent with the
z
axis.
given in Bracewell (2000) have convenient Fourier and Hankel
transforms, respectively, for signal processing applications, but
the sinc and jinc expressions used in Equations 6.9 and 6.5 are
more commonly accepted for the analysis of diffracted pressure
fields generated by finite apertures.
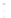
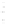
An example of the near-field pressure computed with the
Rayleigh-Sommerfeld integral for the 2
a
by 2
a
square piston
illustrated in Figure 6.3 is shown in Figure 6.4 for
a
= λ. This
pressure calculation evaluates Equation 6.8 on a 121-point by
101-point grid. The smallest value of
NN
−−′
jk
|
rr
|
j
ωρ
π
2
π
π
e
∫
∫
jt
ω
2
px yzt
(, ,,)
=
0
Ue
R
si
n
φφθ
′
dd
′
′
,
0
2
|
rr
−
′
|
−
1
0
π
−
sin(/)
aR
(6.10)
==
′
N
′
that achieves
x
y
2
1
1
0.8
0
0.6
0.4
−1
0.2
0
−2
1.5
0.75
−2
0.75
−1
2
0.5
0
1
0
0.25
0
−0.75
1
−1
0
−1.5
2
−2
x
(units of piston half-width
a
)
z
(units of
a
2
/λ)
y
(units of aperture radius
a
)
x
(units of aperture radius
a
)
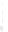
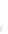
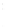
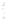
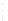
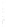
FIGURE 6.4
Near-field pressure computed with the Rayleigh-
Sommerfeld integral for a square 2
a
by 2
a
piston with
a
= λ. he
Rayleigh-Sommerfeld integral achieves a maximum error of 1% in
168.74 seconds when evaluated with
N
x
′
=
N
y
′
= 176 on this 121-point
by 101-point grid.
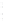
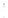
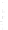
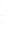
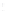
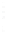
FIGURE 6.5
Spherical shell with aperture radius
a
and radius of cur-
vature
R
= 2
. The spherical shell intersects the
z
axis at
z
= −
R
, the
geometric center is located at (
x ,y,z
) = (0,0,0), and the normal evaluated
at the center of the spherical shell is coincident with the
z
axis.