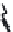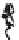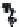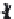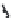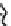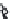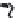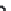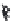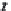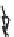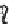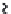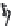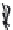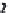Biomedical Engineering Reference
In-Depth Information
all directions in an infinite space). The main advantages of the
Rayleigh-Sommerfeld integral are: (1) this intuitive formulation
is based on the superposition of Green's functions; and (2) this
integral formula is easily evaluated with a computer program.
Disadvantages of the Rayleigh-Sommerfeld integral include rel-
atively long computation times and large errors in the near-field
region due to slow convergence.
The Rayleigh-Sommerfeld integral describing the pressure
radiated from a finite transducer aperture driven by a time-
harmonic input signal is
2
1
0
−1
−−′
jk
|
rr
|
j
ωρ
π
e
∫
0
jt
ω
px yzt
(, ,,)
=
Ue
dS
,
(6 .1)
0
2
|
rr
− ′
|
S
where
p
represents the pressure, (
x ,y,z
) are the observation coor-
dinates in Cartesian space,
t
is the time variable,
j
is
−
, ω is
the radian frequency of the excitation, ρ
0
is the density of the
medium,
U
0
represents the uniform normal particle velocity on
the face of the transducer,
e
j
ω
t
denotes a time-harmonic excita-
tion,
S
indicates that the integration is performed over the sur-
face of the radiating source,
r
represents the coordinates of the
observation point,
r
′ represents the coordinates of the source
point, |
r
−
r
′| is the distance from a source point on the radiating
aperture to the observation coordinates,
k
is the wave number,
and the integrand is the frequency-domain Green's function
for a point source surrounded by a rigid baffle. The formula in
Equation 6.1 admits direct discretization and evaluation for var-
ious piston shapes, including the circular piston, the rectangular
piston, and the spherical shell.
−2
−2
−1
0
1
2
x
(units of piston radius
a
)
FIGURE 6.1
Circular piston with radius
a
centered in the
z
= 0 plane
at (
x
,
y
,
z
) = (0,0,0). The normal at the center of the circular piston is coin-
cident with the
z
axis.
2/
N
are defined for numerical
integration with the midpoint rule,
N
σ
is the number of abscis-
sas in the radial direction, and
N
θ
is the number of abscissas
in the θ′ direction. The double sum in Equation 6.3 evaluates
contributions from the Green's function for a point source in
an infinite baffle, where the distance |
r
−
r
′| is evaluated from
the center
r
′ of each sector on the piston face to an observation
point
r
. The contribution from the Green's function is then mul-
tiplied by the area σ ′Δ σ ′Δθ ′ of each sector and superposed.
where
∆ ′ =
σ
aN
/
and
∆ ′ =
θπ
θ
σ
′
′
6.2.1.1 Circular piston
The Rayleigh-Sommerfeld integral for a circular transducer
(Figure 6.1) excited with a time-harmonic and spatially uniform
normal particle velocity
U
0
is given by
−−
′
jk
|
rr
|
j
ωρ
π
2
π
a
e
∫
∫
0
jt
ω
px yzt
(, ,,)
=
Ue
σ
′
dd
σ
′
θ
,
(6.2)
0
2
|
rr
−
′
|
0
0
1
where the source points are given in cylindrical coordinates
and the observation points are given in Cartesian coordinates
with
0.8
)( sin
2 2 2
− ′ =−′σ ′θ+− ′σ ′θ+
. In Equation
6.2, primed coordinates are source coordinates, unprimed
coordinates are observation coordinates, σ′ is the radial coor-
dinate of the source point, θ′ is the angle between the source
point and the
x
axis, and |
r
−
r
′| represents the distance from
each sampled source point to an observation point. The normal
of the circular piston is coincident with the positive
z
axis, and
the center of the piston is located at the origin of the polar
coordinate system.
Pressures in the near-field region are often numerically
evaluated with the discretized version (Zemanek 1971) of the
Rayleigh-Sommerfeld integral in Equation 6.2 via
|
rr
|
(
x
cos
y
z
0.6
0.4
0.2
0
1.5
0.75
0.75
0.5
0
0.25
−0.75
0
−1.5
z
(units of
a
2
/
λ
)
x
(units of piston radius
a
)
FIGURE 6.2
Simulated near-field pressure obtained with the
Rayleigh-Sommerfeld integral for a circular piston with radius
a
= λ.
The Rayleigh-Sommerfeld integral achieves a maximum error of 1%
in 177.19 seconds when evaluated with
NN
N
N
j
ωρ
π
σ
′
θ
′
−−′
jk
|
rr
|
e
∑
i
∑
,
(6.3)
0
jt
ω
px yzt
(, ,,)
=
Ue
σ
′
∆σσθ
′
∆ ′
===
′
N
212
on this
0
2
|
rr
− ′
|
σ
θ
′
121-point by 101-point grid.
i
=
1
=
1
σ
′
θ
′