Graphics Reference
In-Depth Information
A
1
θ
1
B
A
1
A
2
Y
B
A
1
A
2
A
2
A
1
A
2
⎛
⎝
⎞
⎠
φ
cos
1
θ
2
φ
A
1
A
2
X
A
k
Rotate
(
B, k
φ
,
A
1
)
Z
θ
k
(1
k
)
⋅ θ
1
k
⋅ θ
2
FIGURE 2.22
Interpolating axis-angle representations of (
A
1
, y
1
) and (
A
2
, y
2
)by
k
to get (
A
k
, y
k
), where 'Rotate(a,b,c)' rotates 'c'
around 'a' by 'b' degrees.
2.2.4
Quaternion representation
As discussed earlier, the representations covered so far have drawbacks when interpolating interme-
diate orientations when an object or joint has three degrees of rotational freedom. A better approach
is to use
quaternions
to represent orientation [
5
]. A quaternion is a four-tuple of real numbers, [
s
,
x
,
y
,
z
],
or, equivalently, [
s
,
v
], consisting of a scalar,
s
, and a three-dimensional vector,
v
.
The quaternion is an alternative to the axis and angle representation in that it contains the same
information in a different, but mathematically convenient, form. Importantly, it is in a form that
can be interpolated as well as used in concatenating a series of rotations into a single representation.
The axis and angle information of a quaternion can be viewed as an orientation of an object relative to
its initial object space definition, or it can be considered as the representation of a rotation to apply to an
object definition. In the former view, being able to interpolate between represented orientations is
important in generating key-frame animation. In the latter view, concatenating a series of rotations into
a simple representation is a common and useful operation to perform to apply a single, compound
transformation to an object definition.
Basic quaternion math
Before interpolation can be explained, some basic quaternion math must be understood. In the
equations that follow, a bullet operator represents dot product, and “
” denotes cross-product.
Quaternion addition
is simply the four-tuple addition of quaternion representations, [
s
1
,
v
1
]
þ
[
s
2
,
v
2
]
quaternion multiplication is associative, (
q
1
q
2
)
q
3
¼ q
1
(
q
2
q
3
), but is not commutative,
q
1
q
2
6¼ q
2
q
1
.
½s
1
; v
1
½s
2
; v
2
¼½s
1
s
2
v
1
v
2
; s
1
v
2
þ s
2
v
1
þ v
1
v
2
¼
(2.24)
A point in space,
v
, or, equivalently, the vector from the origin to the point, is represented as [0,
v
].
It is easy to see that quaternion multiplication of two orthogonal vectors (
v
1
v
2
¼
0) computes the
cross-product of those vectors
(Eq. 2.25)
.
½
0
; v
1
½
0
; v
2
¼½
0
; v
1
v
2
if
v
1
v
2
¼
0
(2.25)
The quaternion [1, (0, 0, 0)] is the multiplicative identity; that is,
½s; v½
1
; ð
0
;
0
;
0
Þ ¼ ½s; v
(2.26)




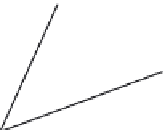










Search WWH ::

Custom Search