Graphics Reference
In-Depth Information
As presented by Witkin, Fleischer, and Barr [
26
]
, energy constraints induce restoring forces based on
arbitrary functions of a model's parameters. The current state of a model can be expressed as a set of
parameter values. These are external parameters such as position and orientation as well as internal
parameters such as joint angles, the radius of a cylinder, or the threshold of an implicit function. They
are any value of the object model subject to change. The set of state parameters will be referred to as
c
.
A constraint is phrased in terms of a non-negative smooth function,
E
(
c
), of these parameters,
and a local minimum of the constraint function is searched for in the space of all parametric values.
The local minimum can be searched for by evaluating the gradient of the energy function and
stepping in the direction of the negative of the gradient,
rE
. The gradient of a function is
the parameter space vector in the direction of greatest increase of that function. Usually the paramet-
ric state set will have quite a few elements, but for illustrative purposes suppose there are only two
state parameters. Taking the energy function as the surface of a height function of those two param-
eters, one can consider the gradient as pointing uphill from any point on that surface (see
Figure 7.39
)
.
Given an initial set of parameters,
c
0
, the parameter function at time zero is defined as
F
(0)
¼ c
0
.
From this it follows that (
d
/
dt
)
F
(
t
)
¼rE
. The force vector in parameter space is the negative of
rE
. Any of a number of numerical techniques can be used
to solve the equation, but a particularly simple one is Euler's method, as shown in Equation
7.92
the gradient of the energy function,
Fðt
iþ
1
Þ¼Fðt
i
ÞhrE
(7.92)
rE
, is usually done numerically by stepping along each dimension in
parameter space, evaluating the energy function, and taking differences between the new evaluations
and the original value.
Determining the gradient,
Three useful functions
As presented by Witkin, Fleischer, and Barr [
26
]
, three useful functions in defining an energy function
are as follows:
direction of increasing E
Energy:
E(P1,P2)
isocontour lines of engery
P2
P1
2D parameter space: P1, P2
gradient of E
FIGURE 7.39
Sample simple energy function.






















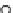





Search WWH ::

Custom Search