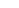Graphics Reference
In-Depth Information
The choice of
v
i
uniformly on the sphere is analogous to choosing an index
k
=
1
n
, except for one thing: When we chose
k
, it was possible that
m
ik
=
0,
that is, the particular path we were following in the Markov chain would con-
tribute nothing to the sum. But when we choose
...
v
i
, we're going to estimate the
arriving radiance at
P
in direction
−
v
i
with a
ray cast
. We'll then
know
that
P
is
visible from whatever point happens to be sending light in that direction toward
P
.
This was one of the great insights of the original path tracing paper: that using ray
casting amounted to a kind of importance sampling for a certain integral over all
surfaces in the scene. (Kajiya performed surface integrals rather than hemispheri-
cal or spherical ones.)
Inline Exercise 31.11:
If the surface at
P
is purely reflective rather than
transmissive, then half of our recursive samples will be wasted. Assume that
transmissive(P)
returns
true
only if the BSDF at
P
has some transmissive
component. Rewrite the pseudocode above to only sample in the positive hemi-
sphere if the scattering at
P
is nontransmissive.
Once again, we can replace the occasional inclusion of
L
e
with an always
inclusion. The code is then
v
):
define estimateL(
C
,
1
2
3
4
5
6
7
8
9
10
−
v
P
= raycast(
C
,
)
u
= uniform(0, 1)
resultSum
=
L
e
v
)
(
P
,
if (
u
< 0.5):
v
i
= randsphere()
integrand
= estimate(
P
,
−
v
i
)
*
f
s
(
P
,
v
i
,
v
)
|
v
i
·
n
P
|
density
=
4
π
resultSum
+=
integrand
/ (0.5
*
density
)
return
resultSum
Now if we suppose that our BSDF can not only be evaluated on a pair of
direction vectors, but also can tell us the scattering fraction (i.e., if the surface
is illuminated by a uniform light bath, the fraction of the arriving power that is
scattered), we can adjust the frequency with which we cast recursive rays:
v
define estimateL(
C
,
1
2
3
4
5
6
7
8
9
10
11
12
13
):
P
= raycast(
C
,
−
v
)
u
= uniform(0, 1)
resultSum
=
L
e
v
)
ρ
= scatterFraction(P)
if (u <
ρ
):
v
i
= randsphere()
Q
= raycast(
P
,
(
P
,
Q
R
v
i
)
integrand
= estimate(
Q
,
−
v
i
)
*
f
s
(
P
,
v
i
,
v
)
|
v
i
·
n
|
L
d
1
4
π
density
=
L
i
v
i
resultSum
+=
integrand
/(
ρ
*
density
)
L
i,s
return resultSum
v
C
P
The second insight we'll take from Kajiya's original paper is that we can write
the arriving radiance from
Q
as a sum of two parts: radiance emitted at
Q
(which
we call
direct light
L
d
at
P
), and radiance arriving from
Q
having been scattered
after arriving at
Q
from some other point, which we call
indirect light
L
i
.Fig-
ure 31.24 shows these. There's no direct light from
Q
to
P
in the figure, since
Q
L
d,s
L
e
Figure 31.24: The light arriving
at P can be broken into direct and
indirect light.