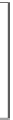Graphics Reference
In-Depth Information
0.6
0
0.5
0.5
0
0
0.6
0.2
0.2
P
=
1
0
0.2
0.5
0.3
0.5
0.2
0
0
0
1
0
3
0.2
0.2
1.0
0.3
0.5
2
0.5
Figure 31.22: A probabilistic FSA with four states,
0, 1, 2,
and
3
;
0
is the start state;
3
is an
absorbing state, and for the remaining states, we have all possible transitions, labeled with
probabilities. A graph like this describes a Markov chain. The transition matrix is shown
as well.
Every row sums to 1 (because when you're in state
i
, you have to transition to
some
state
j
).
Inline Exercise 31.6:
If
P
is an
n
n
matrix with the Markov property just
described, show that the column vector
1
×
1
T
is a right eigenvector
...
of
P
. What's its eigenvalue?
A typical path from state 0 to state 3 in the FSA looks like 01223; the numbers
between the first and last states constitute a subscript sequence that corresponds
to a term in our summation. In this example, the term is
m
12
m
22
b
2
.
(31.85)
Furthermore, such a path has a
probability
of arising from a random walk in
the FSA: We write the product of the probabilities for the edges we traveled. In
our example, this is
p
01
p
12
p
22
p
23
.
(31.86)
We can now describe a general algorithm for computing the sum in Equa-
tion 31.79 (see Listing 31.3).
Listing 31.3: Estimating matrix entries with a Markov chain.
Input: A
2
×
2
matrix
M
and a vector
b
, both with
indices
1
and
2
, and the number
N
of samples to use.
Output: an estimate of the solution
x
to
x
=
Mx
+
b
.
1
2
3
4
5
6
7
8
9
10
P
=
4
×
4
array of transition probabilities, with indices
0,
...
,3
,
as in Figure 31.22.
S
1
=
S
2
=
0
// sums of samples for the two entries of
x
.
repeat
N
times:
s
=
a path in the FSA from state 0 to state 3, so s(0) = 0.