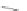Graphics Reference
In-Depth Information
(b) Show that the sequence
Y
1
,
Y
2
,
is a consistent estimator of the mean.
(c) Construct a sequence
Z
n
of unbiased estimators that are
not
consistent. (Hint:
Consistency requires
two
things.)
Exercise 30.7: Rejection sampling.
In many cases where sampling from a
distribution directly is difficult,
rejection sampling
is a last-resort solution that's
guaranteed to work, albeit very slowly in some cases. Figure 30.12 shows the
idea: Drawing a box around the graph of a density function
d
, we select points
uniformly randomly in the box. The
x
-values of these points are treated as samples,
except that
(
x
,
y
)
is rejected (i.e., not used) if
y
...
y
Rejected
(
x
1
,
y
1
)
y
=
d
(
x
)
(
x
2
,
y
2
)
Accepted
d
(
x
)
. In areas where
d
(
x
)
is
large, a sample
(
x
,
y
)
is likely to be accepted; where
d
(
x
)
is small, it's likely to be
rejected. When a sample's rejected, we continue to generate new samples until we
find an acceptable one.
(a) Write a program that uses rejection sampling to generate 10,000 samples from
the distribution
d
(
x
)=
x
on the interval
[
0, 2
]
and plot your results in the form of
a histogram.
(b) What fraction of your attempts at generating samples were rejected?
(c) Repeat with the distribution
d
(
x
)=
>
x
Figure 30.12: We draw a box
around the graph of our probabil-
ity density function d, and choose
a point (x, y) uniformly randomly
in the box. If
(
x
,
y
)
lies under the
graph, we return x; if not, we try
again.
20
1
−
exp(
−
20
)
exp(
−
20
x
)
to see how badly
rejection sampling can work.
(d) Use the
idea
of rejection sampling (pick samples from a too-large space, and
then select only the good ones) to generate points uniformly in the unit disk, and
plot your results.
(e) Use the same idea to sample from the unit ball in 3-space, and the unit ball in
10-space. How well (in terms of rejection) does the last of these work?
(f) Points in the unit ball in any dimension are uniformly distributed in direction
(with the exception of the origin). Use this to take your points-in-a-ball sampler
and make a points-on-a-sphere sampler, being sure to reject the special case of the
origin. Experimentally compare its efficiency to that of the hemisphere sampler
we described. (Depending on your computer's architecture, the comparison could
go either way.)
(g) When you want to rejection-sample the function
x
→
1
+
x
on the interval
[
0, 1
]
,
you draw a box
[
0, 1
]
[
a
,
b
]
for some values
a
and
b
. What are the constraints on
possible values for
a
and
b
? What happens if you make
b
quite large?
×
Exercise 30.8:
Suppose that
X
is a random variable on
[
0, 1
]
with density
e
:[
0, 1
]
→
R
, and that
f
:[
a
,
b
]
→
[
0, 1
]
is a bijective increasing differen-
tiable function.
(a) Show that
t
e
(
f
(
t
))
f
(
t
)
is a probability density on
[
a
,
b
]
.
(b) Suppose that
Y
is a random variable distributed according to
t
→
e
(
f
(
t
))
f
(
t
)
.
→
Suppose that
t
0
∈
[
a
,
b
]
and
x
0
=
f
(
t
0
)
.Howare
Pr
{
t
0
− ≤
Y
≤
t
0
+
}
and
Pr
? This whole problem is
merely an exercise in chasing definitions—there should be no difficult mathemat-
ics involved.
Exercise 30.9:
Use the linearity of expectation repeatedly to show that
Var
[
X
]=
E
[
X
2
]
{
x
0
− ≤
X
≤
x
0
+
}
related, for small values of
E
[
X
]
2
.
Exercise 30.10: Densities.
Suppose that
([
0, 1
]
,
p
)
is a probability space, that
is,
p
is a probability density. We observed that
p
may take on values larger than 1.
In this problem, you'll show that this cannot happen too often. Show that if
p
(
x
)
−
≥
1
M
on the interval
a
M
. Hint: Write out the
probability of the event
[
a
,
b
]
as an integral, and then use the assumption about
p
to give a lower-bound estimate of this integral.
≤
x
≤
b
⊂
[
0, 1
]
, then
b
−
a
<