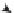Graphics Reference
In-Depth Information
The notion of a random variable can be generalized to that of a
random point
.
If
S
is a probability space, and
Y
:
S
T
is a mapping to another space rather
than the reals, then we call
Y
a “random point” rather than a random variable. The
notion of a probability density applies here as well, but rather than just looking at
an interval
[
a
,
b
]
→
⊂
R
, we must now consider any set
U
⊂
T
; we'll say that
p
Y
is
a pdf for the random variable
Y
if, for every (measurable) subset
U
⊂
T
,wehave
Y
S
Y
2
1
(
U
)
T
t
U
=
u
∈
U
Pr
{
Y
∈
U
}
p
Y
(
u
)
du
.
(30.30)
Y
2
1
(
t
)
In fact, it's usually fairly easy to compute
p
Y
if we know the mapping
Y
by an
argument completely analogous to the one used to find
p
W
.
Figure 30.8: The probability of
U
⊂
T
is
just
the
size
of
In the special case where
S
has a uniform probability density (see Figure 30.8),
the probability of
Y
Y
−
1
(
U
)
⊂
S divided by the size
of S.
U
is just the probability of the set
Y
−
1
(
U
)
∈
⊂
S
, which is
the size of
Y
−
1
(
U
)
divided by the size of
S
.
If we assume that
p
Y
is continuous, then we can compute
p
Y
directly. Consider
the case of a very small neighborhood
U
of some point
t
∈
T
; then the right-hand
side is given by
p
Y
(
u
)
du
≈
size
(
U
)
p
Y
(
t
)
.
(30.31)
u
∈
U
On the other hand, the left-hand side is given by a ratio of sizes as described above,
so
size
(
Y
−
1
(
U
))
size
(
S
)
=
size
(
U
)
p
Y
(
t
)
, and therefore
(30.32)
size
(
Y
−
1
(
U
))
size
(
U
)
1
size
(
S
)
.
p
Y
(
t
)
≈
(30.33)
The first factor in this expression is just an approximation of the change of area
for
Y
−
1
, which is given by the Jacobian of
Y
−
1
at
t
. So in the limit, as
U
shrinks
to a smaller and smaller neighborhood of
Y
(
t
)
, we get
1
size
(
S
)
.
(
Y
−
1
)
(
t
)
p
Y
(
t
)=
|
|
(30.34)
As in the discrete case, we can use
p
Y
as a probability density for the space
T
,
or we can simply use it as the pdf for the random point
Y
.
And once again, if
s
is the identity map, then
p
ι
=
p
,so
the two notions of density—the probability density used in defining a continuum
probability space, and the probability density of a random variable on that space—
are in fact consistent.
Finally, we will again use the notation
X
∼
f
to mean “X is a random variable
distributed according to
f
” which in the continuum case means that
p
X
=
f
. There
is one standard distribution that we'll use repeatedly,
U
(
a
,
b
)
, which is the uniform
distribution on
[
a
,
b
]
, or the constant function
ι
:
S
→
S
:
s
→
1
a
. You'll often see this in forms
b
−
like “Suppose
X
,
Y
∼
U
(
0,
π
)
are two uniform random variables ...”