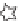Graphics Reference
In-Depth Information
For mathematical convenience, we're going to consider a scene that is
finite,
in the sense that it's contained within some sufficiently large sphere around the
origin; the interior of this sphere we'll assume to be coated with a nonreflective
material so that all light hitting it is absorbed. In a real scene, once light “leaves”
the scene, we ignore it. But for this chapter, it's very useful to have a ray-casting
function that takes a point
P
and direction
d
and returns the first surface point
Q
along the ray starting at
P
and going in direction
d
. If the scene isn't surrounded by
the large sphere, then a ray headed “out of the scene” doesn't hit anything, and the
ray-casting function's value is not defined. So the large black sphere is completely
for mathematical convenience, and it has no impact on the actual transport of light.
To keep the notation simple, we're going to further assume that we're studying
a steady-state situation, one in which there is no time dependence: The luminaires
have all been illuminated for long enough to allow light to scatter throughout the
scene and reach a steady state. Furthermore, we're going to ignore the wavelength
dependence, and study just radiance rather than
spectral
radiance.
Thus, our starting point is a collection of surfaces whose union is the set
M
of all surface points in the scene (including the large enclosing black sphere).
For each point
P
v
o
)
, the bidirectional reflectance
distribution function at
P
, which describes how much light arriving at
P
traveling
in direction
∈
M
,wealsoknow
f
r
(
P
,
v
i
,
−
v
i
becomes light leaving in direction
v
o
(see Chapter 26 for the
formal definition). The symbols
v
o
will be reserved, for this section, to be
unit vectors that point in the same half-plane as the normal vector
n
P
at
P
, that is,
v
i
·
v
i
and
0.
In addition to the scene geometry and reflectance, we assume that we're given
the
illumination
in the scene, described by the emitted radiance at every point of
every luminaire, in every direction; in other words, we're given a function
n
P
≥
0 and
v
o
·
n
P
≥
L
e
:
S
2
L
e
(
P
,
M
×
→
R
:(
P
,
)
→
)
,
(29.1)
v
v
where
L
e
(
P
,
,
the radiance you'd measure if every other luminaire and surface in the scene were
removed, so that no light at all
arrived
at the point
P
, and hence none was reflected.
)
denotes the
emitted
radiance leaving the point
P
in direction
v
v
For a typical point
P
of a typical area luminaire,
L
e
(
P
,
0;
in other words, light radiates only toward the “outward” side of the luminaire.
For luminaires like typical white incandescent lightbulbs, the radiance in all
such outward directions is the same, or
L
e
(
P
,
v
)
is zero if
v
·
n
P
<
0. Because
of the analogy with the light reflected from a Lambertian surface, we'll refer
to such a luminaire as
Lambertian.
)=
C
for
v
·
n
P
>
v
v
2
P
2
Q
1
=
R
(
P
1
,
v
1
)
As we said above, we'll also assume we have a
ray-casting function
(see
Figure 29.1),
S
2
R
:
M
×
→
M
,
(29.2)
where
R
(
P
,
)
is the first point hit by a ray starting at
P
in direction
v
·
n
P
≤
v
1
v
v
.If
0, then
R
(
P
,
)=
P
, that is, a ray
into
a shape hits the shape immediately. If
v
v
·
n
P
>
0, then
R
(
P
,
)
is the point we see by looking in direction
from
P
.
v
v
P
1
More precisely,
R
(
P
,
)
is the farthest point
Q
on the ray from
P
in direction
v
with the property that all points of the ray strictly between
P
and
Q
are in empty
space.
v
Figure 29.1: R
(
P
1
,
v
)=
Q
1
,but
1
v
)=
P
2
.
R
(
P
2
,
2