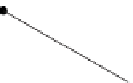Graphics Reference
In-Depth Information
Now we return to the crossroads. Just as cars arrive from the north at a certain rate,
other cars arrive from the south, the east, and the west. To adequately describe all
the arriving cars requires you to keep multiple tallies, one for each arrival direc-
tion. If the crossroads were a more complex intersection, with five, or six, or ten
roads leading into it, you'd need more and more tallies. If cars could arrive in
any
direction, then in the analogy with the probability densities we just discussed the
probability of a car arriving from any
particular
direction would be zero. Instead,
we'd have to talk about a density, where the probability of a car arriving from a
range
of directions was gotten by integrating the density over that range of direc-
tions.
Analogously, light energy can arrive at a point from any direction. The amount
arriving from a range of directions depends in part on how large the range is: If you
narrow the range of directions, you observe less incoming light energy. Indeed, if
you narrow your range of directions to a
single
direction, no energy at all will
arrive from that direction. We speak, therefore, of a
density,
where the amount of
energy arriving in some range of directions is gotten by integrating this density
over that range of directions.
Just as the energy from a single direction is zero, the energy arriving at any sin-
gle
point
is also zero. To get something meaningful, we must consider the energy
arriving over some small region. Once again, this is done with a density: We posit
a function whose integral, over a small region,
1
gives the amount of energy arriv-
ing there.
All of this will be made more explicit in Section 26.7; for now the key idea is
that our model of light moving around in a scene will be based on a density func-
tion whose arguments range over several continua: time, position, and direction.
To define a “range of directions” for light arriving at a surface in 3-space, we need
to define a notion of “solid angle” in
R
3
in analogy with the notion of angle in
R
2
.
A
P
An angle in
R
2
is usually defined by a pair of rays at a point
P
(see
Figure 26.18). If we look at a unit circle
C
around
P
, there's an arc
A
contained
between the rays. The length of the arc
A
is the measure of the angle.
We can revise this definition slightly, and say that the arc
Ais
the angle.
Clearly, if you know the arc
A
and the point
P
, you can find the two rays, and
vice versa, so the distinction is a small one. But we can then generalize, and say
that an angle at
P
is
any
subset
2
of the unit circle
C
at
P
. The measure of the angle
is the total length of all the pieces of the subset. In practice, there are typically
a finite number of pieces—usually just one—so this isn't a large generalization.
Finally, it's often convenient to not talk about points of the circle
C
, but about
points on the unit circle, or unit vectors. For any point
X
in
C
, we can form the
unit vector
v
=
X
Figure 26.18: An angle at the
point P.
P
.Given
v
and
P
, it's easy to recover
X
=
P
+
v
. So our
revised notion of an “angle at
P
” is this: An angle at
P
is either a subset of the unit
circle
C
with center
P
, or a subset of the set
S
1
of all unit vectors.
−
1. We'll generally use the term “region” to indicate a portion of a surface, and the term
“area” to indicate the size of that region (i.e., something whose units are m
2
), although
we'll occasionally use terms like “pixel area” to indicate a region.
2.
Any
measurable
subset [Roy88]. See Chapter 30.