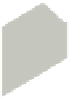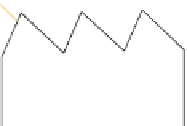Graphics Reference
In-Depth Information
triangles, it's possible to address the cache-miss problem quite effectively. The
obvious solution to the “overdraw” problem, however, is view-dependent: If we
can sort the triangles front to back, we can minimize overdraw. But such a sort
order will likely break up the clusters that addressed the vertex-cache problem.
Nonetheless, this front-to-back approach provides the core of the algorithm. We
can find a front-to-back order for the triangles by creating a graph whose nodes
are triangles and where there's a directed edge from
t
1
to
t
2
if
t
1
obscures (partly or
completely)
t
2
. Performing a topological sort on this graph gives a drawing order,
assuming that the graph is acyclic. We'll return to the problem of cycles presently.
Nehab et al. [NBS06] have developed a solution that incorporates the best of
both approaches, in the presence of backface culling: They create clusters that are
large enough that only a small amount of cache-missing is introduced (compared
to the optimal), but which also substantially reduce overdraw when the clusters
are drawn in a particular order. Their approach relies on three key ideas.
1.
If two polygons' normal vectors have a dot product of
1, then their sort
order will have no impact on overdraw, because whenever one is front-
facing, the other will be back-facing, and hence culled. For dot products
greater than
−
−
1, the chance of overdraw increases with increasing dot
product.
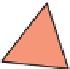
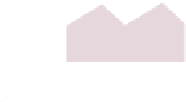
Figure 25.30: The sort order
of the blue and red polygons
is immaterial because of back-
face culling; the blue polygon
obscures the green from some
viewpoints, but the green never
obscures the blue.
2. If their normal vectors have a positive dot product, it's possible that one
obscures the other from many viewpoints, but the other never obscures the
first. In this case, any sort order where the obscuring polygon comes before
the obscured reduces overdraw.
3. The preceding observations are still true even for planar clusters of poly-
gons, and even if the clusters are nearly planar rather than planar.
Figure 25.30 shows these situations. Notice that if the mesh is convex, then
any
sort order will minimize overdraw, because for a convex mesh, there's never
any overdraw at all. Even for the nonconvex wave-shaped rooftop mesh of Fig-
ure 25.31, it's still possible to draw the polygons in an order that creates no over-
draw. With these examples in mind, the algorithm has two broad steps: First, we
create nearly planar connected clusters of triangles using a
k
-means-like clustering
algorithm [HA79]; then we determine a sort order for the clusters by creating a
graph whose nodes are the clusters and in which there's a directed edge from
c
1
to
c
2
if
c
1
obscures
c
2
more than
c
2
obscures
c
1
(averaged over all possible points of
view). The edges are given weights depending on how much more
c
2
obscures
c
1
than
c
1
obscures
c
2
. We then attempt a topological sort on this graph, using edge
weights to break any cycles that arise.
1
3
2
2
3
1
Figure 25.31: Draw-
ing the rooftop regions of
the building in increasing numer-
ical order, and using backface
culling, will prevent overdraw no
matter what the viewpoint.
25.6.2.1 Clustering
The user must provide a number,
k
, of clusters to compute;
k
provides a tradeoff
between vertex-cache efficiency and overdraw efficiency. (The authors report that
between 10 and 100 clusters suffice for models on the order of 100,000 triangles.)
We then select
k
random triangles and grow clusters from them. In general, a
k
-means algorithm has two steps that are alternated: adding items to a cluster
based on a “distance” to some representative for the cluster, and updating the
representative. For clustering points in a plane, the representative is typically the
centroid of the cluster, the distance is Euclidean, and at each iteration, each item
is added to the cluster whose center, from the last iteration, is nearest.