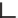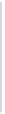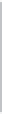Graphics Reference
In-Depth Information
may lie outside the cell, and furthermore, in areas where the surface is nearly pla-
nar the Hermite data for a cell may create a quadratic error function that is nearly
degenerate (i.e., one whose zero-set is a whole line or plane) so that finding a
minimizer is numerically unstable. Their work addresses this by careful numeri-
cal analysis, although their solution requires an ad hoc constant.
A mesh can be “broken” in all sorts of ways. Consider something as simple as a
(hollow) triangle
ABC
in the plane. If we consider the edges as oriented as
AB
,
BC
, and
CA
, then the oriented boundary of the triangle, where the endpoint of
each edge is counted as a
+
1 and the starting point as a
1, is empty. But if the
edges are oriented as
AB
,
BC
, and
AC
, then the oriented boundary is 2
C
−
2
A
;
if we were computing the boundary as a way to check whether the triangle was
watertight, we'd find that it wasn't. And if we used the oriented edges to compute
normal vectors, the misoriented edge
AC
would cause problems with inside/out-
side determination. In a mesh whose representation contains an edge table, an
algorithm closely related to the one for consistently orienting faces can be used to
repair the edge table.
Often meshes created with rendering speed in mind have characteristics that
generate problems, like T-junctions or nonwatertightness. Sometimes those cre-
ated with the best intentions, like the Utah teapot, have problems. (The original
teapot had no bottom!) So, while nice models are best to work with, we often
encounter
polygon soup
—a collection of polygons that
nearly
form a nice sur-
facelike mesh—and we want to be able to make the most of what we've got. One
example of this is in scanning, where a scanner may produce a great many points
on a surface, and may even organize those points into triangles, but the triangles
gathered from different views of the model may be inconsistent because of prob-
lems with registration of the views, or changing occlusion, etc. Such triangle soups
need to be cleaned up to form consistent models for use in the rest of the graphics
pipeline.
Ju [Ju04] has used his dual contouring for Hermite data to address this last
problem. The ideas in the approach are simple, and the results are particularly
attractive, so we sketch the method briefly here. The input is a collection of poly-
gons; the output is a surface mesh that's consistent, in some way, with the input
polygons. Figure 25.26 shows the process (in 2D) in the case where the input mesh
is already
a closed polygon; in this case, the original mesh is reconstructed almost
exactly, although it has been translated by an amount smaller than the grid cell.
−
(a)
(b)
(c)
(d)
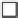
Figure 25.26: (Following [Ju04],
Figure 3.) Ju's model-repair
method. (a) A model, embedded
in a fine grid. (b) The grid edges
that intersect the model, stored in
an oct tree. Each cell touches an
even number of such edges. (c)
Signs at grid points (indicated by
light or dark shading) generated
from the set of intersection edges.
(d) The model reconstructed by
contouring the sign data.
The steps in the process are as follows.
1. The polygon soup is embedded in a uniformly spaced grid, and grid edges
that intersect any polygon are marked as intersection edges. The cells con-
taining such edges are stored in an oct tree. The choice of a fixed grid size
implicitly represents a choice about aliasing: An empty polygon soup, and
soup consisting of a single tetrahedron that fits entirely within one grid
cell, will produce the same (empty) output. Thus, these two “signals” end
up as aliases of each other.
2. The intersection edges are used to generate signs at the grid points in such
a way that each intersection edge exhibits a sign change. This may be