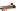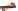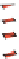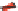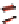Graphics Reference
In-Depth Information
⎡
⎣
⎤
⎦
1
4
661011001
616101100
601610110
610160011
444004000
404400400
400440040
440040004
3
2
3
2
3
2
3
2
1
4
1
4
1
4
9
1
16
V
=
V
.
(23.16)
More generally, for a vertex of degree
n
, there are 2
n
+
1rowsin
V
and the subdi-
vision matrix is a
(
2
n
+
1
)
(
2
n
+
1
)
matrix. Letting
V
n
denote the neighborhood
coordinates for a vertex of degree
n
, we can write
×
V
n
=
S
n
V
n
,
(23.17)
where the matrix
S
n
is of the appropriate size. Everything about Catmull-Clark
subdivision can be determined by studying the matrix
S
. Halstead et al. [HKD93]
carry this out in some detail.
As an example of what one can derive, if we look at some vertex
v
in a mesh,
during repeated subdivision
v
will approach some point
v
∞
. (This can be proved
by looking at powers of
S
; the web materials for this chapter do so explicitly.) The
limit point point
v
∞
for
v
under repeated subdivision is
v
∞
=
n
2
v
+
4
j
e
j
+
j
f
1
n
(
n
+
5
)
,
(23.18)
where the primes indicate one level of subdivision. (This is determined by looking
at eigenvectors of
S
.) Notice that
v
need not be a vertex of the original mesh. If,
after three levels of subdivision, we insert a new face point, we can call this point
v
, find its neighboring face and edge points, and apply the limit formula above.
We can now make three observations.
First, the formula for computing the limit point does exactly the same compu-
tation with the
x
-,
y
-, and
z
-coordinates. In fact, it works in any dimension at all,
and we can think about subdivision surfaces one coordinate at a time.
Second, if the initial mesh consists of the integer lattice in the
xy
-plane (i.e.,
all integer points are vertices, and the unit-length vertical and horizontal segments
joining them are the edges), then a single subdivision operation produces the half-
integer lattice, two subdivisions produce the quarter-integer lattice etc.
Third, if we alter the integer lattice by replacing
(
0, 0, 0
)
with
(
0, 0, 1
)
,the
limit surface shown in Figure 23.6 is very simple. In fact, just as for subdivision
curves,
it turns out that this limit surface is actually identical to the cubic B-spline
basis function. In particular, if
(
x
,
y
,
z
)
is on the limit surface, then
B
(
x
,
y
)=
z
,
where
B
is the basis function.
This means that, at least in areas where the mesh has standard lattice con-
nectivity, the limit subdivision surface is the same as the B-spline surface defined
by those control points. Since code for computing and rendering such surfaces is
widely available, this is very convenient. In any neighborhood of an exceptional
vertex (i.e., one whose degree is different from four), the limit surface is
not
sim-
ilar to a B-spline, and we have to compute the surface by repeated subdivision.
Stam [Sta98] discusses the limit shape both at and away from exceptional points.
Figure 23.6: (Top) The initial
mesh consists of the integer lat-
tice with one point raised. (Mid-
dle) The first and second levels of
subdivision. (Bottom) The cubic
B-spline basis function whose
control points are the vertices
of the original control mesh, for
comparison.