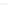Graphics Reference
In-Depth Information
y
5
f
(
x
)
y
5
f
(
v
)
20
200
150
0
100
50
20
−
0.5
0
0.5
500
0
500
−
−
5
5
v
y
g
(
x
)
y
g
(
)
6
1
4
0
2
1
0
−
−
0.05
0
0.05
−
500
0
500
y
5
f
(
x
)
g
(
x
)
y
5
f
(
v
)
g
(
v
)
1500
20
1000
0
500
0
−
20
−
0.5
0
0.5
−
500
0
500
Figure 18.54: The Taj Mahal data (top left) is multiplied by a narrow comblike function
(left middle—note the different scale on the x-axis!), with closely spaced peaks, to produce
the “sampled” version at the bottom left. The Fourier transform of the original signal
(top right) is convolved with the transform of the comblike signal (middle right, comblike
with widely spaced peaks) to produce the transform of the sampled signal (bottom right),
showing overlapping replicates of the transform of the original signal.
Figure 18.54 shows the situation, which we now explain. Let's say that the
original Taj Mahal data is described by a function
x
f
(
x
)
. The “sampled”
version, which we'll call
h
, was generated by multiplying
f
by a function
g
that
approximated a comb function, that is, that consisted of a bunch of narrow peaks
of area 1, with spacing about 1
→
/
200, to produce a signal
h
=
fg
. This means that
h
=
f
g
. But since
g
is an approximation of the comb function, its Fourier trans-
form is an approximation of the transformed comb function, which is just another
comb function. Since the spacing for
g
is about 1
200, the spacing for
g
is about
200. So
h
is just
f
convolved with a comblike function with spacing of 200. That
convolution consists of multiple copies of
f
, one at each comb tooth, summed up.
This explains the approximate periodicity of the Fourier transform
h
.
/
L
2
(
R
)
, and its
We now further examine the relationship between a function,
f
∈
samples at integer points, which define a function
f
2
(
Z
)
. We need a new
∈
if
f
(
definition:
f
is
strictly band-limited at
ω
ω
)=
0for
ω ≥ ω
0
. Note the shift
from “
>
”to“
≥
.” The main result of this section is as follows.