Graphics Reference
In-Depth Information
q
5
direction (
R
)
3
(
V
2
2
V
0
)
V
2
Ray
R
e
2
s
5
origin (
R
)
2
V
0
r
5
s
3
e
1
V
1
e
1
Triangle
T
V
0
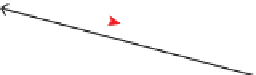
Figure
15.5:
Variables
for
computing
the
intersection
of
a
ray
and
a
triangle
(see Listing 15.16).
normals. We structure our implementation to return the weights to the caller. The
caller could use either those or the distance traveled along the ray to find the
intersection point. We return the distance traveled because we know that we will
later need that anyway to identify the closest intersection to the viewer in a scene
with many triangles. We return the barycentric weights for use in interpolation.
Figure 15.5 shows the geometry of the situation. Let
R
be the ray and
T
be
the triangle. Let
e
1
be the edge vector from
V
0
to
V
1
and
e
2
be the edge vector
from
V
0
to
V
2
. Vector
q
is orthogonal to both the ray and
e
2
. Note that if
q
is also
orthogonal to
e
1
, then the ray is parallel to the triangle and there is no intersection.
If
q
is in the negative hemisphere of
e
1
(i.e., “points away”), then the ray travels
away from the triangle.
Vector
s
is the displacement of the ray origin from
V
0
, and vector
r
is the cross
product of
e
1
. These vectors are used to construct the barycentric weights,
as shown in Listing 15.16.
Variable
a
is the rate at which the ray is approaching the triangle, multiplied
by twice the area of the triangle. This is not obvious from the way it is computed
here, but it can be seen by applying a triple-product identity relation:
s
and
Let
d
=
R.direction()
Let
area
=
|
e
2
×
e
1
|/
2
a
=
e
1
·
q
=
e
1
·
d
×
e
2
=
d
·
e
2
×
e
1
=
−
(
d
·
n
)
·
2
·
area
,
(15.4)
since the direction of
e
1 is opposite the triangle's geometric normal
n
.The
particular form of this expression chosen in the implementation is convenient
because the
q
vector is needed again later in the code for computing the barycen-
tric weights.
There are several cases where we need to compare a value against zero. The
two
epsilon
constants guard these comparisons against errors arising from lim-
ited numerical precision.
The comparison
a <= epsilon
detects two cases. If
a
is zero, then the ray is
parallel to the triangle and never intersects it. In this case, the code divided by zero
many times, so other variables may be infinity or not-a-number. That's irrelevant,
since the first test expression will still make the entire test expression
true
.If
a
is
negative, then the ray is traveling away from the triangle and will never intersect
it. Recall that
a
is the rate at which the ray approaches the triangle, multiplied by
the area of the triangle. If
epsilon
is too large, then intersections with triangles
e
2
×