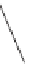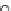Graphics Reference
In-Depth Information
The blending mode
BlendFunc(SRC_ALPHA, ONE_MINUS_SRC_ALPHA)
yields
d
c
=
s
α
·
s
c
+(
1
−
s
α
)
·
d
c
,
(14.20)
which is linear interpolation by
s
α
. Our coverage value at each point is either 0
or 1, as befits the physical model of the star: At every point sample the rectan-
gle enclosing the star is either completely opaque and blocks all light from the
background, or completely transparent and allows the background to be seen.
Rendering under such a binary coverage scheme with a single sample per pixel
will generate aliasing, where the edges of the star appear as stair steps in the
image. If we increase the number of samples per pixel, we will obtain a better
estimate of the fraction of the star that covers an individual pixel. For example, in
Figure 14.27, the outlined pixel is about 50% covered by the star and 50% covered
by the background. However, the estimate would be poor if we used three samples
instead of four, and even the four samples from the diagram can produce an error
of
04
5
0% blue
2 4
5
50% blue
12.5% coverage for pixels with less even coverage. Taking many samples per
pixel is of course an expensive way to evaluate partial coverage by analytically
defined shapes.
±
44
5
100% blue samples
Figure 14.27: An ideal blue vec-
tor star shape rasterized on a
low-resolution
We've seen this problem before, with texture maps encoding reflectance. The
MIP-mapping solution developed in Chapter 20 works for coverage as well as
reflectance. Imagine a prefiltered coverage map for the star rectangle in which
the outlined pixel in Figure 14.27 is a single
texel
(one pixel in a texture-map
image). Its coverage value is the integral of binary coverage over that texel, which
is
s
α
=
0. 3. This integral is called
partial coverage.
Equation 14.20 holds for
partial coverage as well as binary coverage; in this case it is called the
over oper-
ator
because it represents the image of a partially covering
s
lying over the back-
ground
d
.
Order matters, however. The over operator assumes that we're rendering sur-
faces in back to front order (the Painter's Algorithm described in Section 36.4.1)
so that we always composite nearer objects
over
farther ones.
Note that
s
α
encodes the fraction of coverage, but not the locations of that
coverage within the texel. One interpretation of
s
α
is that it is the probability that a
sample chosen uniformly at random within the texel will hit the opaque part of the
rectangle instead of the transparent part. For the star, the probability remains at the
extremes of 0 and 1 except at texels along the edge. For other shapes, nearly every
texel encodes some kind of edge. Consider a screen door, for example. We might
paint a texture that has
s
α
as 1 and 0 in alternating rows and columns at the highest
resolution. Such a texture has maximum spatial frequencies, so it could produce
significant aliasing. However, after a single MIP level, the texture contains entirely
fractional values.
An advantage of the probabilistic interpretation of partial coverage is that it
allows us to describe the result of successive applications of blending for different
surfaces without explicitly representing the high-frequency coverage mask in the
result image
d
. For example, we can render the back wall as viewed through two
identical screen doors by computing the final destination color
d
c
for each channel
c
pixel
grid.
The
boxes
of
the
grid
are
pixels.
The
circles
represent
samples
at
which
we
are
computing
coverage.
∈
r, g, b as
d
c
=
s
α
·
s
c
+(
1
−
s
α
)
·
d
c
(14.21)
d
c
=
s
α
·
d
c
s
c
+(
1
−
s
α
)
·
(14.22)
s
α
)
2
d
c
.
=(
1
−
s
α
)
s
α
·
s
c
+(
1
−
·
(14.23)