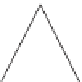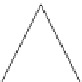Graphics Reference
In-Depth Information
0
2
14
14.5.1.1 Indexed Triangle Meshes
Indexed triangle meshes (see Chapter 8) are a pervasive surface representation in
graphics. The minimal representation is an array of vertices and a list of indices
expressing connectivity. There are three common base schemes for the index list.
These are called
triangle list
(or sometimes
soup
),
triangle strip,
and
triangle
fan
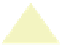
representations. Figures 14.13 through 14.15 describe each in the context of
counterclockwise triangle winding and 0-based indexing for a list describing
n
6
8
12
5
9
7
1
13
3
4
10
11
Figure 14.13: A
triangle list,
also
known as a
triangle soup,
con-
tains
3
n indices. List elements
3
t
,3
t
+
1
, and
3
t
+
2
are the
ordered indices of triangle t.
>
0 triangles.
14.5.1.2 Alternative Mesh Structures
For each representation there is a corresponding nonindexed representation as a
list whose element
j
is
vertex[index[j]]
from the indexed representation. Such
nonindexed representations are occasionally useful for streaming large meshes
that would not fit in core memory through a system. Because they duplicate stor-
age of vertices (which are frequently much larger than indices), these representa-
tions are out of favor for moderate-sized models.
One can also construct quadrilateral or higher-order polygon meshes following
comparable schemes. However, triangles have several advantages because they are
the 2D simplex: Triangles are always planar, define an unambiguous barycentric
interpolation scheme, never self-intersect, and are irreducible to simpler polygons.
These properties also make them slightly easier to rasterize, ray trace, and sam-
ple than higher-order polygons. Of course, for data such as city architecture that
is naturally modeled by quadrilaterals, a triangle mesh representation increases
storage space without increasing model resolution.
1
3
5
0
2
4
6
Figure 14.14: A
triangle strip
contains n
+
2
indices. The
ordered indices of triangle t are
given as follows. For even t, use
list elements t, t
+
2
,t
+
1
.For
odd t, use list elements t, t
+
1
,
t
+
2
.
3
7
5
4
8
14.5.1.3 Adjacency Information
Some algorithms require efficient computation of adjacency information between
faces, edges, and vertices on a mesh. For example, consider the problem of ren-
dering the contour of a convex mesh for a line-art program. Each edge is drawn
only if it is on the contour. An edge lies between two faces. It is on the contour
if exactly one face is oriented toward the viewer. We can make this determination
more quickly if we augment the minimal indexed mesh with additional informa-
tion describing faces, edges, and adjacency. Under that representation, we might
directly iterate over edges (instead of triangles) and expect constant-time access
to the two faces adjacent to each edge.
Adjacency information depends only on topology, so it may be precomputed
for an animated mesh so long as the mesh does not “tear apart” under animation.
Listing 14.4 gives a possible representation for a mesh with full adjacency infor-
mation. In the listing, all the integers in the
Vertex
,
Edge
, and
Face
classes are
indices into the arrays at the bottom of the class definition. Because faces are ori-
ented, the order of elements matters in their
vertices
index arrays. This is the
modern array-based equivalent of a classic mesh data structure called the
winged
edge polyhedral representation
[Bau72] (see Chapter 8).
There are several ways to encode the edge information within these data struc-
tures. One is to consider the directed
half-edges
that each exist in one face. A true
edge that is not on the boundary of the edge would then be a pair of half-edges. The
half-edge representation offers the advantage of retaining orientation information
when it is reached by following an index from a face. It has the disadvantage of
2
6 3
4
10
2
9
0
0
12
11
13
1
5
1
14
Figure 14.15: A triangle soup
pentagon on the left, and the
more efficient triangle fan model
on the right. A
triangle fan
con-
tains n
+
2
indices. List elements
0
,t
+
1
,t
+
2
are the ordered
indices of triangle t (with indices
taken mod n
+
2
).