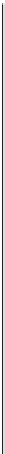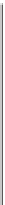Graphics Reference
In-Depth Information
Because we'll be homogenizing in a moment, we can multiply through by
f
−
n
and instead use the matrix
⎡
⎤
f
−
n
0
0
0
⎣
⎦
0
f
−
n
00
M
pp
=
.
(13.16)
0
0
f
n
0
0
−
(
f
−
n
)
0
w
The derivation of this matrix is slightly messy and not particularly informative;
we cover it in this chapter's web materials. For now, all we need to do is verify
that it does in fact transform the frustum between the near and far planes (
z
=
c
and
z
=
(0, 1)
(
c
, 1)
(
2
1, 1)
w
5
1
1, respectively) in the standard perspective view volume to the standard
parallel view volume. We'll do so by looking at corners.
−
z
The only interesting part of the unhinging matrix of Equation 13.15 is in the
zw
-plane, so it's worth looking at that more closely, remembering that after this
transformation, all points will be homogenized (i.e., projected radially from
the origin onto the
w
=
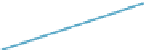
1 line in the diagram). Figure 13.11 shows the slice
of the view volume before transformation. The thick blue segment at the right
on the
w
=
1 line represents the
zw
-slice of the view frustum between the near
and far clipping planes. The thick red segment at the left is the part of the view
cone between the near plane and the eye. The red point on the
y
-axis is the
eye. The transformation tilts and stretches the
w
=
1 line (see Figure 13.12).
Points at
z
=
Figure 13.11: Side view of frus-
tum and view volume in the zw-
plane before unhinging.
w
1 (the far clipping plane) remain fixed. The near clipping plane
is transformed to lie on the
z
=
0 line. The eye is transformed onto the
w
=
0
line. After homogenization (see Figure 13.13), the front clipping plane remains
at
z
=
0, while the eyepoint is sent to “infinity on the
z
-axis,” causing the lines
that used to meet at the eye to become parallel lines that “meet at infinity
on the
z
-axis” (i.e., parallel lines that are parallel to the
z
-axis). These three
constraints on the transformation are enough to uniquely determine the matrix
(see Exercise 13.9).
−
(0, 1)
(
c
, 1)
(
2
1, 1)
w
5
1
z
Figure
13.12:
After
applying
M
pp
.
w
Consider the upper-right front corner of the frustum. It's at the location
(
−
c
,
−
c
,
c
)
. (Recall that
c
=
−
n
/
f
is negative, so
−
c
is positive.) Under the
transformation
M
pp
it becomes
⎡
⎤
⎡
⎤
⎡
⎤
w
5
1
f
−
n
0
0
0
−
c
−
c
(
f
−
n
)
⎣
⎦
·
⎣
⎦
⎣
⎦
0
f
−
n
00
−
c
c
1
−
c
(
f
n
)
cf
+
n
−
z
=
.
(13.17)
0
0
f
n
0
0
−
(
f
−
n
)
0
−
(
f
−
n
)
c
Figure 13.13: After
homogenization.
Homogenizing, we get
11
cf
+
n
−
(
f
−
n
)
c
1
T
=
1101
T
,
(13.18)
the upper-right front corner of the standard perspective view volume, as promised,
where the last step depends on
cf
+
n
=
n
−
f
f
+
n
=
0.