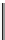Graphics Reference
In-Depth Information
v
1
x
x
u
2
e
2
Mx
x
e
1
u
1
v
2
M
2
1
x
x
KM
2
1
x
x
Figure 10.6: Multiplication by the matrix
M
takes
e
1
and
e
2
to
u
1
and
u
2
, respectively,
so multiplying
M
−
1
does the opposite. Multiplying by
K
takes
e
1
and
e
2
to
v
1
and
v
2
,so
multiplying first by
M
−
1
and then by
K
, that is, multiplying by
KM
−
1
,takes
u
1
to
e
1
to
v
1
,
and similarly for
u
2
.
Inline Exercise 10.11:
(a) Find a matrix transformation sending
e
1
to
0
4
and
e
2
to
1
.
(b) Use the relationship of matrix inverse to the inverse of a transform, and the
formula for the inverse of a 2
1
2 matrix, to find a transformation sending
0
4
×
to
e
1
and
1
1
to
e
2
as well.
As Inline Exercise 10.11 shows, we now have the tools to send the
standard
basis vectors e
1
and
e
2
to any two vectors
v
1
and
v
2
, and vice versa (provided
that
v
1
and
v
2
are independent, that is, neither is a multiple of the other). We can
combine this with the idea that composition of linear transformations (performing
one after the other) corresponds to multiplication of matrices and thus create a
solution to a rather general problem.
Problem:
Given independent vectors
u
1
and
u
2
and any two vectors
v
1
and
v
2
, find a linear transformation, in matrix form, that sends
u
1
to
v
1
and
u
2
to
v
2
.
Solution:
Let
M
be the matrix whose columns are
u
1
and
u
2
. Then
T
:
R
2
R
2
:
x
→
→
Mx
(10.21)
sends
e
1
to
u
1
and
e
2
to
u
2
(see Figure 10.6). Therefore,
S
:
R
2
R
2
:
x
M
−
1
x
→
→
(10.22)
sends
u
1
to
e
1
and
u
2
to
e
2
.
Now let
K
be the matrix with columns
v
1
and
v
2
. The transformation
R
:
R
2
R
2
:
x
→
→
Kx
(10.23)
sends
e
1
to
v
1
and
e
2
to
v
2
.
If we apply first
S
and then
R
to
u
1
, it will be sent to
e
1
(by
S
), and thence to
v
1
by
R
; a similar argument applies to
u
2
. Writing this in equations,
R
(
S
(
x
)) =
R
(
M
−
1
x
)
(10.24)
=
K
(
M
−
1
x
)
(10.25)
=(
KM
−
1
)
x
.
(10.26)