Graphics Reference
In-Depth Information
The definition of linearity guarantees that for any linear transformation
T
,we
have
T
(
0
)=
0
: If we choose
v
=
w
=
0
and
α
=
1, the definition tells us that
T
(
0
)=
T
(
0
+
1
0
)=
T
(
0
)+
1
T
(
0
)=
T
(
0
)+
T
(
0
)
.
(10.2)
Subtracting
T
(
0
)
from the first and last parts of this chain gives us
0
=
T
(
0
)
.This
means that
translation
—moving every point of the plane by the same amount—
is, in general,
not
a linear transformation except in the special case of translation
by zero, in which all points are left where they are. Shortly we'll describe a trick
for putting the Euclidean plane into
R
3
(but
not
as the
z
=
0 plane as is usually
done); once we do this, we'll see that certain linear transformations on
R
3
end up
performing translations on this embedded plane.
For now, let's look at only the plane. We assume that you have
some
famil-
iarity with linear transformations already; indeed, the serious student of computer
graphics should, at some point, study linear algebra carefully. But one can learn a
great deal about graphics with only a modest amount of knowledge of the subject,
which we summarize here briefly.
In the first few sections, we use the convention of most linear-algebra texts:
The vectors are arrows at the origin, and we think of the vector
u
v
as being
identified with the point
(
u
,
v
)
. Later we'll return to the point-vector distinction.
For any 2
Mv
is a linear transformation from
R
2
to
R
2
. We refer to this as a
matrix transformation.
In this chapter, we look
at five such transformations in detail, study matrix transformations in general, and
introduce a method for incorporating translation into the matrix-transformation
formulation. We then apply these ideas to transforming objects
and
changing coor-
dinate systems, returning to the clock example of Chapter 2 to see the ideas in
practice.
×
2matrix
M
, the function
v
→
y
x
We begin with five examples of linear transformations in the plane; we'll refer to
these by the names
T
1
,
...
,
T
5
throughout the chapter.
Example 1: Rotation.
Let
M
1
=
cos
30
◦
−
sin
30
◦
Before
sin
30
◦
cos
30
◦
and
y
R
2
:
x
y
M
1
x
y
=
cos
30
◦
−
x
y
.
sin
30
◦
T
1
:
R
2
→
→
(10.3)
sin
30
◦
cos
30
◦
Recall that
e
1
denotes the vector
1
and
e
2
=
0
; this transformation sends
x
0
1
e
1
to the vector
cos
30
◦
, which are vectors that are 30
◦
counterclockwise from the
x
- and
y
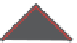
-axes, respectively (see Figure 10.1).
and
e
2
to
−
sin
30
◦
cos
30
◦
sin
30
◦
There's nothing special about the number 30 in this example; by replacing 30
◦
with any angle, you can build a transformation that rotates things counterclock-
wise by that angle.
After
Figure 10.1: Rotation by
30
◦
.