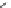Graphics Reference
In-Depth Information
2
f
2
1
v
2
f
0
P
v
0
4
0
f
1
0
3
1
2
2
v
1
3
1
4
0
5
Figure 9.2: The point P is in the triangle with vertices v
0
,v
1
, and v
2
, where the function has
values f
0
,f
1
, and f
2
, respectively. What value should we assign to the point P?
This “continuous extension” of
f
has analogs for other situations. Before we
look at those, let's examine some of the properties. First, the value of the interpo-
lated function at noon or midnight each day (
t
i
)isjust
f
i
; it doesn't depend at all
on the values at noon or midnight on the other days. Second, the value at noon on
one day influences the shape of the graph only for the 12 hours before and the 12
hours after. Third, the interpolated function is in fact continuous.
Now let's consider interpolating values given at discrete points on a surface.
Since we often use triangle meshes in graphics to represent surfaces, let's suppose
that we have a function whose values are known at the vertices of the mesh; the
value at vertex
i
is
f
i
. How can we “fill in” values at the other points of all the
triangles in the mesh?
By analogy, we use barycentric coordinates. Consider a point
P
in a triangle
with vertices
v
0
,
v
1
, and
v
2
(see Figure 9.2); we can define
f
(
P
)=
c
0
f
0
+
c
1
f
1
+
c
2
f
2
(9.7)
where
(
c
0
,
c
1
,
c
2
)
are the barycentric coordinates of
P
with respect to
v
0
,
v
1
, and
v
2
.
Once again, the interpolated function has several nice properties. First, the
value at the vertex
v
i
is just
f
i
; the value along the edge from
v
i
to
v
j
(assuming
they are adjacent) depends only on
f
i
and
f
j
; thus, for a point
q
on such an edge,
it doesn't matter which of the two triangles sharing the edge from
v
i
to
v
j
is used
to compute
f
(
q
)
—the answer will be the same! Second, the value
f
i
at vertex
v
i
again influences other values only
locally,
that is, only on triangles that contain
the vertex
v
i
. Third, the interpolated function is in fact continuous.
The remainder of this chapter investigates this idea of interpolating across
faces, its relationship to barycentric coordinates, and some applications.
The discussion so far has been somewhat abstract; we'll now write some code to
implement these ideas. Let's start with a simple task.
Input:
• A triangle mesh in the form of an
n
×
3 table,
vtable
, of vertices
•A
k
3 table,
ftable
, of triangular faces, where each row of
ftable
con-
tains three indices into
vtable
×