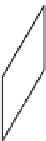Graphics Reference
In-Depth Information
For an oriented manifold-with-boundary mesh, the boundary will consist of
exactly the edges we identified above as “boundary edges.” In general, an oriented
mesh with no boundary edges is called
closed.
8.3.1.4 Operations on Manifold-with-Boundary Meshes
Manifold-with-boundary meshes support operations like vertex and face insertion
and deletion. The efficiency of each operation depends on the implementation. If
the representation is simply vertex tables and face tables, then insertion is O
(
1
)
,
and deletion (after the “exchange with the last item in the list” trick) is too. If we
maintain a neighbor list for each vertex, then insertion becomes O
(
T
)
, where
T
is
the number of triangles, as does deletion.
Note that computing the boundary of such a mesh can be done in O
(
T
)
time.
(Use a hash table to count the number of times each edge appears, with sign. If the
edge appears zero times, delete it from the hash table.) But one can also maintain
a record of the boundary during insertions and deletions so that reporting it at any
timeisanO
(
1
)
operation.
Just as in the 1D case, we sometimes encounter shapes that are not well rep-
resented by manifolds or manifolds with boundary. The two cubes shown in
Figure 8.10 share a vertex which is a nonmanifold vertex; two cubes sharing an
edge are similarly nonmanifold. There is an important difference between the two
cases, however: It's easy to encounter a nonmanifold vertex in the course of con-
structing a manifold with boundary (see Figure 8.11). But once we construct a
nonmanifold edge (one with three or more faces meeting it), it can never become
a manifold edge through further additions.
Figure 8.10: The shared vertex is
nonmanifold: No neighborhood
looks planar.
Each vertex in the
directed-edge
structure also contains a reference to one of
the edges containing it (see Figure 8.12). This allows one to compute the neigh-
borhood of the vertex (all edges and triangles that meet it) in time proportional to
the size of the neighborhood.
Campagna et al. [CKS98] show how this structure can be extended to handle
non-manifold vertices and edges, and how to trade time for space by simplifying
the structure for very large meshes.
Figure 8.11: The pyramid at left
has six faces; the bottom square
is divided into two triangles that
you cannot see. If we construct
the pyramid so that after four
triangles have been added, it
appears as shown at the right,
then the apex vertex is neither
an interior vertex nor a bound-
ary vertex according to the def-
initions, so this shape is neither
a manifold nor a manifold with
boundary. Once we add another
face, it becomes a manifold with
boundary, and when we add the
last face, it becomes a manifold.
v
b
Vertices
x
a
y
a
z
a
e
r
e
q
x
b
y
b
z
b
e
q
next
…
neighbor
Directed edges
v
a
v
b
e
neighbor
e
next
e
previous
prev
e
r
v
a
Figure 8.12: The directed-edge data structure (following Figures 4 and 5 of [CKS98]). A
directed edge stores a reference to its starting and ending vertex, to the previous and next
edges, and to its neighbor. For each real edge of the mesh, there are two directed edges, in
opposite directions. Each vertex stores its coordinates and a reference to one of the directed
edges that leaves it.