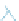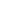Graphics Reference
In-Depth Information
The cross product is
anticommutative,
that is,
v
v
(the labeling and
ordering of the subscripts was chosen to make this self-evident). It's distributive
over addition and scalar multiplication, but not associative. One of the main uses
of the cross product is that
×
w
=
−
w
×
v
×
w
=
v
w
|
sin
θ|
(7.33)
where
is the angle between
v
and
w
. That means that half the length of the
cross product is the area of the triangle with vertices
(
0, 0, 0
)
,
(
v
x
,
v
y
,
v
z
)
, and
(
w
x
,
w
y
,
w
z
)
.
The cross product can be generalized to dimension
n
; in dimension
n
, it's a
product of
n
θ
1 vectors (which explains why the
n
=
3 case is the most often
used). Aside from dimension 3, our most frequent use will be in dimension 2,
where it's a “product” of one vector. The cross product of the vector is
−
v
x
v
y
=
−
.
v
y
v
x
×
(7.34)
×
This cross product has an important property: Going from
v
to
v
involves a
rotation by 90
◦
in the same direction as the rotation that takes the positive x-axis
to the positive y-axis
. Because of this, it's sometimes also denoted by
v
⊥
.
In the same way, going from
v
to
w
to
v
u
w
describes a
right-handed coor-
dinate system,
one in which placing your right-hand pinkie on the first vector and
curling it toward the second makes your thumb point in the direction of the third
(see Figure 7.8). In general, in
n
dimensions, the cross product
z
of
n
×
v
−
1 vectors
v
1
,
...
,
v
n
−
1
lies in a line perpendicular to the subspace containing
v
1
,
...
,
v
n
−
1
.
w
The length of
z
is
(
n
1
)
-dimensional volume of the pyramid-
like shape whose vertices are the origin and the endpoints of
v
i
. Assuming this
volume is nonzero,
z
is oriented so that
v
1
,
v
2
,
−
1
)!
times the
(
n
−
Figure 7.8: The uvw directions
form a right-handed coordinate
system.
,
v
n
−
1
,
z
is “positively oriented”
in analogy with the right-hand rule in three dimensions.
...
7.6.4.2 Dot Product
From linear algebra, you're familiar with the
dot product
of two
n
-vectors
v
and
w
, defined by
v
·
w
=
v
1
w
1
+
v
2
w
2
+
...
+
v
n
w
n
.
(7.35)
This is sometimes denoted
; in this form, it's usually called the
inner prod-
uct.
The dot product is used for measuring angles. If
v
and
w
are unit vectors,
then
v
,
w
v
u
v
·
w
=cos(
θ
)
,
(7.36)
where
θ
is the angle between the vectors (Figure 7.9). This is most often used in
the form
u
·
v
w
1
=cos
−
1
θ
(7.37)
1
v
w
which gives the angle between any two nonzero vectors, expressed as a number
between 0 and
π
, inclusive.
R
2
for a moment. The function
Fix the vector
w
∈
Figure 7.9: The dot product of
unit vectors gives the cosine of
the angle
φ
w
:
R
2
→
R
:
v
→
·
w
v
(7.38)
θ
between them.