Graphics Reference
In-Depth Information
and
y
are both zero, the returned value is zero. This makes atan2
discontinuous at
the origin,
as well as along the negative
x
-axis. On the negative
x
-axis, the IEEE
version of atan2
(
y
,
x
)
returns either
+
,
2
π
−π
depending on whether
y
=+
0or
or
,
1
−
0. The only tricky part is remembering that
y
comes first. You can remember
this by knowing that if
(4, 2)
−π<θ<π
, then
atan2
(sin
θ
,
cos
θ
)=
θ
.
(7.16)
We'll use atan2 not only in programs, but also in equations.
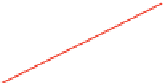
Figure 7.3: The Cartesian plane,
in which points are specified by x-
and y-coordinates.
The Cartesian plane shown in Figure 7.3 is a model for Euclidean geometry: All
of the axioms of geometry hold in the Cartesian plane, and we can use our geo-
metric intuition to reason about it. A tabletop (or to be more accurate, an infi-
nite tabletop) is also a model for Euclidean geometry. The difference between
the two is that each point of the Cartesian plane has a pair of real numbers—its
coordinates
—associated to it. This lets us transform geometric statements like
“the point
P
lies on the lines
,
P
2
” to algebraic statements, like “the coordi-
nates of the point
P
satisfy these two linear equations.” We can, of course, draw
two perpendicular lines on the infinite tabletop, declare them to be the
x
- and
y
-axes, place equispaced tick marks along each, and use perpendicular projection
onto these lines to define coordinates. But the choices we made—which line to
call the
x
-axis, which to call the
y
-axis, what point to use as the origin, etc.—were
arbitrary.
3
It's important to distinguish between the properties of a point or a line,
and the properties of its coordinates; the underlying geometric properties don't
change when we change coordinate systems, while numerical properties of the
coordinates
do
change. In Figure 7.4, you can see that the point
P
is on the line
1
and
Figure 7.4: The Cartesian plane
with multiple coordinate systems.
—that's a
geometric
property; it's true independent of any coordinate system.
P
As an example of coordinate-dependent properties, the coordinates of
P
in the
black coordinate system are
(
3, 5
)
, while in the blue coordinate system they are
(
2, 2
)
. Similarly, the equation of the line
M
in the black coordinate system is
y
=
5,
while in the blue coordinate system it's
x
+
y
=
4. Thus, the point's coordinates
and the line's equation are coordinate-dependent. But the fact that the point is on
the line is coordinate-independent: Although
P
's coordinates and
Q
's equation are
different in the two systems, the black coordinates of
P
satisfy the black equation
for
, and similarly for the blue.
From now on when we speak of “the coordinates of a point,” it will always be
with respect to some coordinate system; much of the time the coordinate system
will be obvious and we won't mention it. For example, in
R
2
, the set of ordered
pairs of real numbers, the “standard” coordinates of the point
(
x
,
y
)
are just
x
and
y
.
Figure 7.5: The coordinates of M
in each coordinate system are the
average of the coordinates of P
and Q in that coordinate system;
thus, the
geometric
operation of
finding the midpoint of a seg-
ment corresponds to the
algebraic
operation of averaging coordi-
nates,
independent of what coor-
dinate system we use.
Suppose (see Figure 7.5) we have the points
P
=(
2, 5
)
and
Q
=(
4, 1
)
in the
plane, where the coordinates are with respect to the coordinate system drawn in
horizontal and vertical black lines. If we
average
the coordinates of these points
3. Indeed, Descartes did not even require that the two axes be perpendicular, although we
now always choose them so.