Graphics Reference
In-Depth Information
36.5.2.1 Sutherland-Hodgman 2D Clipping
There are many clipping algorithms. Perhaps the simplest is the 2D variation of
Sutherland's and Hodgman's [SH74] algorithm. It clips one (arbitrary)
source
polygon against a second, convex
boundary
polygon (see Figure 36.16). The
algorithm proceeds by incrementally clipping the source against the line through
each edge of the boundary polygon, as shown in Listing 36.3.
Inline Exercise 36.5:
Construct an example input polygon which, when
clipped against the unit square by the Sutherland-Hodgman algorithm, pro-
duces a polygon with degenerate edges (i.e., edges that meet at a vertex
v
with
an exterior angle of 180
◦
).
For viewport clipping, Sutherland-Hodgman is applied to a projected polygon
and the rectangle of the viewport. For projected polygons that have significant area
outside the viewport, clipping to the viewport is an efficient alternative to scissor-
testing each sampled point. The algorithm is further useful as a general geometric
operation in many contexts, including modeling shapes in the first place.
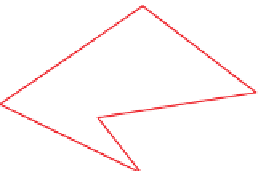
Figure 36.16: The red input poly-
gon is clipped against the con-
vex blue boundary polygon; the
result is the boundary of the yel-
low shaded area.
Listing 36.3: Pseudocode for Sutherland-Hodgman clipping in 2D.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
// The arrays are the vertices of the polygons.
// boundaryPoly must be convex.
function polyClip(Point sourcePoly[], Point boundaryPoly[]):
for each edge (A, B) in boundaryPoly:
sourcePoly = clip(sourcePoly, A, Vector(A.y-B.y, B.x-A.x))
return sourcePoly
// True if vertex V is on the "inside" of the line through P
// with normal n. The definition of inside depends on the
// direction of the y-axes and whether the winding rule is
// clockwise or counter-clockwise.
function inside(Point V, Point P, Vector n):
return (V - P).dot(n) > 0
// Intersection of edge CD with the line through P with normal n
function intersection(Point C, Point D, Point P, Vector n):
distance = (C - P).dot(n) / n.length()
t = (D - C).length()
return D
*
t+C
*
(1-t)
// Clip polygon sourcePoly against the line through P with normal n
function clip(Point sourcePoly[], Point P, Vector n):
Point result[];
// Add the last point, if it is inside
D = sourcePoly[sourcePoly.length - 1]
Din = inside(D, P, n)
if (Din): result.append(D)
for (i = 0; i < sourcePoly.length; ++i) :
C = D, Cin = Din
D = sourcePoly[i]
Din = inside(D, P, n)