Global Positioning System Reference
In-Depth Information
Fig. 4. Three dimensional vector representation for a receiver and four satellites.
3.4 Kleusberg's algorithm
Kleusberg (1994) provided a vector algebraic solution for GPS. The geometry of the 3-D
positioning is shown in figure 4. It begins with the fundamental equation 6 for range estimates.
It also uses di
ff
erence equation given below analogous to equation 4 between two satellite
measurements.
2
2
2
2
2
2
(
x
−
x
i
)
+ (
y
−
y
i
)
+ (
z
−
z
i
)
−
(
x
−
x
1
)
+ (
y
−
y
1
)
+ (
z
−
z
1
)
= (
r
i
−
r
1
) =
d
i
(21)
=
This represents a sheet of hyperboloid. We can find three such hyperboloids for
i
2, 3 and
4 that can be solved for determining the receiver position. Mathematically, there will be two
solutions though one of which can be discarded from the knowledge of the earth's proximity.
Let
b
2
,
b
3
,
b
4
be the known distances from satellite 1 to satellites 2, 3, 4 along unit vectors
e
2
,
e
3
,
e
4
. From the cosine law for triangle 1
−
i
−ρ
,
r
i
=
b
i
+
r
1
−
2
b
i
r
1
e
1
·
e
i
(22)
Squaring equation 21 and equating with
r
i
of equation 22, we get
b
i
−
d
i
2
r
1
=
(23)
d
i
+
b
i
e
1
·
e
i
(
)
(
)
(
)
Using satellite pairs
1, 2
,
1, 3
and
1, 4
; we can get three equations for
r
1
as follows:
b
2
−
d
2
b
3
−
d
3
b
4
−
d
4
b
2
e
1
·
e
2
=
b
3
e
1
·
e
3
=
(24)
d
2
+
d
3
+
d
4
+
b
4
e
1
·
e
4
e
1
.
Some rewritings result in the two scalar equations as follows:
The only unknown in the above equation is the unit vector
=
e
1
·
f
2
u
2
and
=
e
1
·
f
3
u
3
(25)










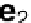

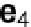

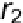

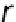

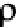
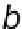
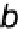
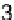
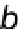
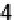





Search WWH ::

Custom Search