Global Positioning System Reference
In-Depth Information
Anchor node
Regular node
Observed range
Actual range
Linear Form LOP
Hyperbolic LOP
Anchor node
Regular node
Observed range
Actual range
Linear Form LOP
Hyperbolic LOP
100
100
80
80
60
60
40
40
20
20
0
0
−20
−20
−20
0
20
40
60
80
100
120
−20
0
20
40
60
80
100
X
X
(a)
(b)
55
Anchor node
Regular node
Observed range
Actual range
Linear Form LOP
Hyperbolic LOP
50
Anchor node
Regular node
Observed range
Actual range
Linear Form LOP
Hyperbolic LOP
45
150
40
35
100
30
50
25
0
20
−50
15
−100
10
−5
0
5
10
15
20
25
30
−50
0
50
100
150
200
X
X
(c)
(d)
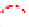
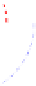
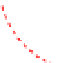
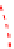
Fig. 3. The hyperbolic and linear form LOPs for unequal noise presence. (a) The general case
when two observed circular LOPs physically intersect. (b) The case when observed circular
LOPs do not intersect due to underestimation of the ranges. (c) The case when observed
circular LOPs do not intersect but overlap completely due to overestimation of the ranges.(d)
The case when ranging errors are of opposite signs.
Assuming equal noise presence, it is useful to explore paired measurements rather than
individual ranges to mitigate the e
ff
ect of noise.
As the di
ff
erence of the range estimates
=
equate to actual di
r
1
), the LOP for the
receiver position is found by the locus of positions maintaining constant di
ff
erence for equal noise presence (
e.g.
,
r
2
−
r
1
r
2
−
erence from the
pair of satellites. Hence, the hyperbolic LOP of the receiver can be found independent of the
noise parameters as shown in Fig. 2 and formulated below:
ff
2
2
2
2
(
x
−
x
2
)
+ (
y
−
y
2
)
−
(
x
−
x
1
)
+ (
y
−
y
1
)
=
(
r
2
−
r
1
)
(4)
=
After algebraic manipulations, it takes the general hyperbolic form as follows for
p
1
(
)
p
2
=(
)
, and
r
1
−
r
2
=
0, 0
,
a
,0
c
.
x
2
2
y
2
c
2
4
a
−
−
a
2
c
2
1
=
(5)
−




















































































































































































































Search WWH ::

Custom Search