Digital Signal Processing Reference
In-Depth Information
−
( )
+
( )
=
1
α
+
1
α
f
γγ
k
n
1
f
n
n
,
k
2
2
N
+
1
1
(9.14)
γγ
n
=
k
∈∈
{ }
g
k
n
,
k
0,
,
N
,
∑
N
1
γγ
n
l
N
+
1
l
=
0
where
·
1
is the 1-norm of a vector and α ∈[-1,1] is a user-defined weighting parameter.
Observe that
γ
[
n
]
1
=
f
[
n
]
1
; for α = -1 we get the NLMS algorithm, and for α = 1 we
get the PNLMS algorithm.
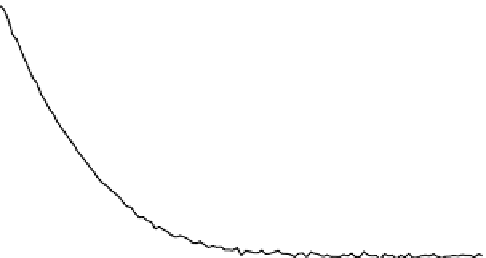
Proportionate adaptation rules are compared in Figures 9.3 to
9.5
. In Figure 9.3,
NLMS, PNLMS, MPNLMS, and IPNLMS are compared for channel identification, in
which just over half of the channel coefficients are zero, and most of the rest are small.
In
Figures 9.4
and 9.5, a similar comparison is made for equalization. The magnitudes
of the optimal equalizer taps are presented in Figure 9.4, sorted for easy analysis of the
level of sparsity, and the learning curves are presented in Figure 9.5. Observe that for
both the identification problem and the equalization problem, all proportionate adapta-
tion algorithms see a performance gain. However, PNLMS and MPNLMS were origi-
nally developed for echo cancellation, in which as many as 90% of the channel taps may
be essentially zero. In wireless identification or equalization, the optimal filters are not
10
1
NLMS
MPNLMS
10
0
10
-1
PNLMS
10
-2
IPNLMS
10
-3
0
200
400
600
800
1000
1200
Symbol number
FIgure 9.3
A demonstration of the convergence improvement of adaptive identification of
wireless channels due to the use of proportionate adaptation. The algorithms considered are all
in the normalized LMS family: NLMS [29], PNLMS [18], MPNLMS [39], and IPNLMS [42]. The
channel had five of eleven nonzero taps, and thus was only somewhat sparse.






















Search WWH ::

Custom Search