Geoscience Reference
In-Depth Information
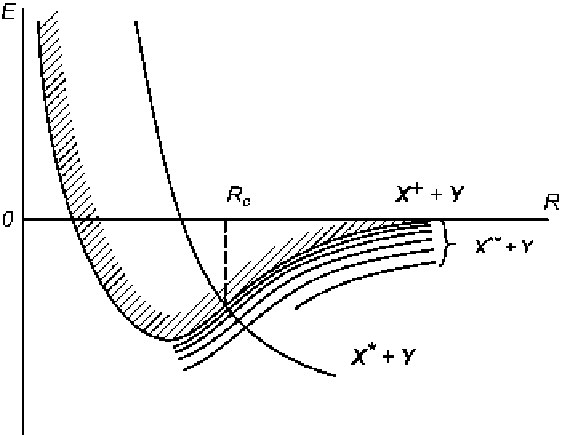
Fig. 1.3
The same as for Fig.
1.2
with a quasi-crossing of the potential curves in the point
R
c
Coulomb refinement levels) is solved in the special model case, then the set of
Rydberg terms is replaced by a system of the parallel lines, and the diabatic
dissociative term is also linearized. In the framework of the Demkov-Osherov
contour integral method (Demkov and Osherov
1968
), the problem is reduced to
multiplying the probabilities to stay on the dissociative term at each point of pseudo-
crossing (followed by a summation of the exponents of all these points). This
approach is reasonable if the ionization and the transitions to highly excited states
are determined by the behavior of the system near the avoided crossing
R
c
in the
small neighborhood
L
R
, which is the parameter of the problem. Upon reaching the
point,
R
D
R
c
of the bound state disappears, merging with a continuous spectrum.
The ionization cross section in this approximation is equal to R
c
.
In the 1970s, the majority of model theoretical studies of the AI process were
performed without a set of avoided crossings that occur right up to the potential
curve of the quasi-molecule across the border of the molecular ion continuum.
Attempts to take them into account in the framework of the traditional approaches
based on individual review of each pseudo-crossing for highly excited states
were not successful. In this regard, we developed a method that implements the
“diffusion-based approach to the collision ionization of excited atoms” (Devdariani
et al.
1988
). We are talking about the diffusion over the quasi-molecule state
energies in a single act of the collision: the main collision parameter is the binding
energy of the excited electron. During the “diffusion,” the initial single quasi-
molecule term is transformed into a “burning” type of conic section at large
distances (
R
!1
) with decrease in
R
(Fig.
1.4
).