Nonlinear Projections - Transformations and Projections in Computer Graphics - page 163

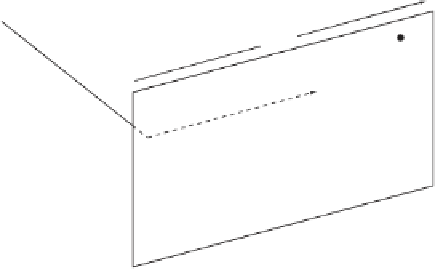
shows the cylinder unrolled. Point P is located in the same place in space, but its
projection has moved with the opening of the cylinder.
Figure 4.21c shows the geometry of the problem. We assume that the dimensions
of the original rectangle are 2 Y

2 Z . When rolled into a cylinder of radius R ,the
perimeter of the cylinder satisfies 2 πR =2 Y ,so R = Y/π . Consider an arbitrary
three-dimensional point P =( x, y, z ) viewed by the observer. When the cylinder is
eventually unrolled, P will be projected to a point P ∗ =( x ∗ ,y ∗ ,z ∗ ) and our problem is
to determine the coordinates of P ∗ as functions of x , y , z , Y ,and Z .

×

z

P

z

P 2Y

P *

P *

y

2Z

y

x

x

cut
here

The x = R

plane

Q

(b)

(a)

x = R

P

y

D

unroll
here

z

P * P

R

P *

z

Z

II

θ

I

R

x

III

IV

D

Z

Y

Y

Y= R π

(c)

(d)

Figure 4.21: A 360 ◦ Panoramic Projection.

The x ∗ coordinate is trivial to determine. The figure shows that all the points on
the unrolled cylinder have the same x coordinate. We can set it to R or, even simpler,
to zero. The y ∗ coordinate should equal the length of the arc subtended by θ ,whichis
Rθ .Angle θ depends on the x and y coordinates of P but not on its z coordinate. The