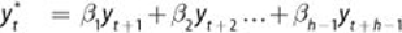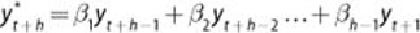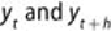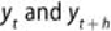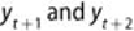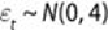Database Reference
In-Depth Information
,
, and
the
.
In other words, after linear regression is used to remove the effect of the variables
between on , the PACF is the correlation of what remains.
For , there are no variables between . So the PACF(1) equals
ACF(1). Although the computation of the PACF is somewhat complex, many
software tools hide this complexity from the analyst.
For the earlier example, the PACF plot in
Figure 8.4
illustrates that after lag
2, the value of the PACF is sharply reduced. Thus, after removing the effects
of , the partial correlation between is relatively small.
Similar observations can be made for h = 4, 5, …. Such a plot indicates that
an AR(2) is a good candidate model for the time series plotted in
Figure 8.2
.
In fact, the time series data for this example was randomly generated based on
where
.
Figure 8.4
Partial autocorrelation function (PACF) plot
Because the ACF and PACF are based on correlations, negative and positive values
are possible. Thus, the magnitudes of the functions at the various lags should be
considered in terms of absolute values.
8.2.3 Moving Average Models
For a time series, , centered at zero, a
moving average model of order q
,
denoted MA(q), is expressed as shown in
Equation 8.9
.