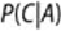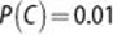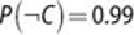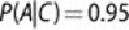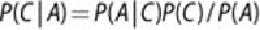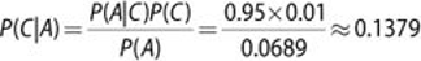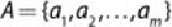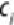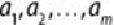Database Reference
In-Depth Information
a positive result in 95% of the cases in which the disease is actually present, and
it returns a positive result in 6% of the cases in which the disease is not present.
Furthermore, 1% of the entire population has this disease. What is the probability
that Mary actually has the disease, given that the test is positive?
Let
C
= {having the disease} and
A
= {testing positive}. The goal is to solve the
probability of having the disease, given that Mary has a positive test result,
. From the problem description,
,
,
and
.
Bayes' theorem defines
. The probability of testing
positive, that is
, needs to be computed first. That computation is shown in
According to Bayes' theorem, the probability of having the disease, given that Mary
has a positive test result, is shown in
Equation 7.11
.
That means that the probability of Mary actually having the disease given a positive
test result is only 13.79%. This result indicates that the lab test may not be a good
one. The likelihood of having the disease was 1% when the patient walked in the
door and only 13.79% when the patient walked out, which would suggest further
tests.
A more general form of Bayes' theorem assigns a classified label to an object
with multiple attributes
such that the label corresponds to the
largest value of
. The probability that a set of attribute values
(composed
of
variables
) should be labeled with a classification label
equals
the probability that the set of variables
given
is true, times the
probability of
divided by the probability of
. Mathematically, this is
shown in
Equation 7.12
.