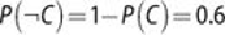Database Reference
In-Depth Information
schedule, he checks in at least two hours before his flight only 40% of the time.
Suppose John did not receive an upgrade on his most recent attempt. What is the
probability that he did not arrive two hours early?
Let
C
= {John arrived at least two hours early}, and
A
= {John received an
upgrade}, then
¬
C
= {John did not arrive two hours early}, and
¬
A
= {John did not
receive an upgrade}.
John checked in at least two hours early only 40% of the time, or
.
Therefore,
.
The probability that John received an upgrade given that he checked in early is
0.75, or
.
The probability that John received an upgrade given that he did not arrive two
hours early is 0.35, or
. Therefore,
.
The probability that John received an upgrade
can be computed as shown in
7.8
Thus, the probability that John did not receive an upgrade . Using
Bayes' theorem, the probability that John did not arrive two hours early given that
he did not receive his upgrade is shown in
Equation 7.9
.
Another example involves computing the probability that a patient carries a
disease based on the result of a lab test. Assume that a patient named Mary took
a lab test for a certain disease and the result came back positive. The test returns