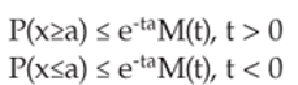Database Reference
In-Depth Information
Distribution Inequalities
When working with random numbers and distributions there are several
useful inequalities to consider. These distributions are useful for providing
bounds on estimates, as shown in several parts of Chapter 10.
The first two inequalities place an upper bound on the probability that a
random variable will take on a value larger than
a
. The first, known as the
Markov inequality states that P(X ≥ a) ≤ E[X]/a.
Using (X-E[X])
2
as the random variable in Markov's inequality leads to the
Chebyshev inequality: P(|X-E[X]| ≥ a) ≤ Var(X)/a
2
. This is also written as
P(|X-E[X]| ≥k×s) ≤ 1/k
2
, where s is the standard deviation of the random
variable.
Although sharper bounds can usually be obtained if the actual distribution
of the random variable is known, both of the inequalities do not require the
assumption of a particular distribution. They only require that the first or
second moment be finite.
If X is taken to be the sum of
n
independent random variables then Chernoff
Bounds can be obtained for the random variable. Chernoff Bounds provide
upper and lower bounds for a random variable as follows:
Where M(t) is the moment generating function introduced in the previous
section. For a given distribution, t is selected for each side of the bound to
minimize the probability.
Finally, Jensen's inequality deals with functions of random variables. It
states that the expectation of a function of X will always be at least as large
as a function of the expectation of X: E[f(X)] ≥f(E[X]).
Random Number Generation
Before continuing on to the sampling approaches and aspects of sampling,
a discussion of random number generators is required. The default random
number generator for many languages is the Linear Congruential Generator