Fundamentals of mass transport in the microscale - Micromixers Fundamentals Design and Fabrication - page 29

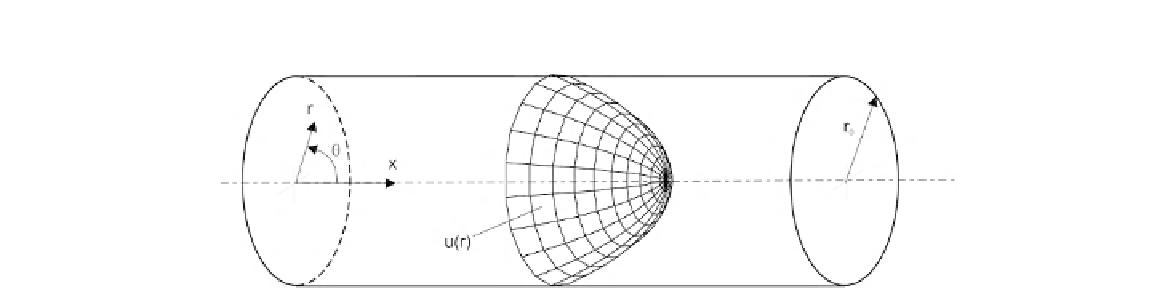
FIGURE 2.9

Model for determination of Taylor dispersion in a circular channel.

where u is the mean velocity as listed in Table 2.2 . For this capillary, the general equation for
conservation of species (2.22) , also called the convective/diffusive equation, can be formulated in the
cylindrical coordinate system with no species generation ( r g ¼ 0) as:

vc
vt þ

vc
vz ¼

2 c

u ð r Þ D V (2.42)

where

r

v 2
vq 2 þ

v 2
vx 2 :

1
r

v
vr

v
vr

1
r 2

2

V ¼ þ (2.43)

The boundary and initial conditions of (2.42) are:
d c
d r

r¼r 0 ¼

0

(2.44)

c j x / N ¼ 0

c j t¼ 0 ¼ c 0 ð r ; q ; x Þ:

Equation (2.42) can be solved numerically with the above boundary and initial condition for c ( r , q , x , t )).
Taylor derived an analytical asymptotic solution for (2.42) as follows .
If the observer moves along the flow with the mean velocity u , we can consider a new axial
coordinate x *:

x ¼ x ut: (2.45)

x þ Substituting x ¼ ut into (2.42) results in:

D 1
r

r vc
vr

v 2 c
vq 2 þ

v 2 c
vx

vc
vt þ½

vc
vx ¼

v
vr

1
r 2

u ð r Þ u þ : (2.46)

2

For (2.46) , the previous boundary and initial conditions with the new spatial variable x * apply. In
order to solve (2.46) analytically, the following asymptotic assumptions are made:

ðt[r 0 =DÞ; Radial diffusion is complete thus, vc=vtz 0 ;

Axial diffusion is negligible compared to axial convection

D v 2 c
vx

thus, D v 2 c
vx

vc
vx [

ð½ u ð r Þ u Þ;

2 ¼

0 ;

2