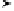Cryptography Reference
In-Depth Information
y
•
P
+
Q
P
•
x
Q
Fig. 9.4
Point addition on an elliptic curve over the real numbers
draw the tangent line through
P
and obtain a second point of intersection between
this line and the elliptic curve. We mirror the point of the second intersection along
the
x
-axis. This mirrored point is the result
R
of the doubling. Figure 9.5 shows the
y
P
•
x
•
2
P
Fig. 9.5
Point doubling on an elliptic curve over the real numbers
doubling of a point on an elliptic curve over the real numbers.
You might wonder why the group operations have such an arbitrary looking form.
Historically, this
tangent-and-chord
method was used to construct a third point if
two points were already known, while only using the four standard algebraic op-
erations add, subtract, multiply and divide. It turns out that if points on the elliptic
curve are
added
in this very way, the set of points also fulfill most conditions neces-
sary for a group, that is, closure, associativity, existence of an identity element and
existence of an inverse.
Of course, in a cryptosystem we cannot perform geometric constructions. How-
ever, by applying simple coordinate geometry, we can express both of the geomet-