Cryptography Reference
In-Depth Information
solutions of the equations. For example, the point (
x
=
r
,
y
= 0) fulfills the equation
of a circle and is, thus, in the set. The point (
x
=
r
/
2
,
y
=
r
/
2) is not a solution to the
polynomial
x
2
+
y
2
=
r
2
and is, thus, not a set member. An
elliptic curve
is a special
type of polynomial equation. For cryptographic use, we need to consider the curve
not over the real numbers but over a finite field. The most popular choice is prime
fields
GF
(
p
) (cf. Sect. 4.2), where all arithmetic is performed modulo a prime
p
.
Definition 9.1.1
Elliptic Curve
The
elliptic curve
over
Z
p
,p
>
3
,isthesetofallpairs
(
x
,
y
)
∈
Z
p
which fulfill
y
2
x
3
+
a
≡
·
x
+
b
mod
p
(9.1)
together with an imaginary
point of infinity
O
, where
a
,
b
∈
Z
p
a
3
+ 27
b
2
and the condition
4
·
·
= 0mod
p.
The definition of elliptic curve requires that the curve is nonsingular. Geometri-
cally speaking, this means that the plot has no self-intersections or vertices, which
is achieved if the discriminant of the curve
16(4
a
3
+ 27
b
2
) is nonzero.
For cryptographic use we are interested in studying the curve over a prime field
as in the definition. However, if we plot such an elliptic curve over
−
Z
p
, we do not get
anything remotely resembling a curve. However, nothing prevents us from taking an
elliptic curve equation and plotting it over the set of real numbers.
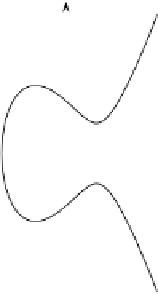
Example 9.3.
In Figure 9.3 the elliptic curve
y
2
=
x
3
−
3
x
+ 3 is shown over the real
numbers.
y
x
Fig. 9.3
y
2
=
x
3
−
3
x
+ 3 over
R