Image Secret Sharing - Visual Cryptography and Secret Image Sharing - page 382

1; 2; ;H; i = 0; 1; ;k), k is the number of shares. We dene the matrix
operations of Lagrange polynomials with degree k in the Galois field:

k X k Y

xx i
x j x i

L k (x) =

A i (14.6)

i=0 j=0;i6=j

where (x i ;A i ) is the feature point, A i ( (i = 0; 1; ;k)) are matrices of size
WH, the elements being nonnegative, x i is a real number and xi i x j (i j).
Our novel idea for color image sharing using Lagrange interpolation is the
following. We utilize the secret image and a few (< n) other chosen innocuous
images to build the Lagrange interpolation polynomial. We then construct
new images based on this interpolation to obtain a total of n images. We now
can use all the innocuous images and the new reconstructed images as the
shares of the secret image. And the secret image is not distributed but it can
be always reconstructed using the requisite number of shares. So our novelty is
in the construction of new shares based on the secret image and some chosen
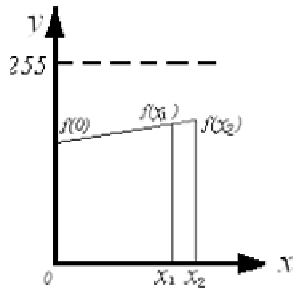
innocuous images. We now provide the details of the scheme. In Figure 14.2,
assume that the secret image that we desire to share is at the position x = 0.

(a)l= 2 (b)l= 3

FIGURE 14.2
Image sharing based on the Lagrange interpolation in (a) and (b).

In Figure 14.2(a), we position an innocuous image at x 2 . We can now
compute many new shares with the parameters in the interval (x 2 d;x 2 +d),
d > 0, (we have used d max = x 2 x 4 ). Without loss of generality, we select the
parameter at the position x 1 as our newly created share (based on 0 and x 2 ).
We now consider the images at x 2 and x 1 as the shares of the secret image
at 0. For the reconstruction of the secret, we can collect the two shares, we
calculate the coecients of Lagrange interpolation polynomial first and then