Biomedical Engineering Reference
In-Depth Information
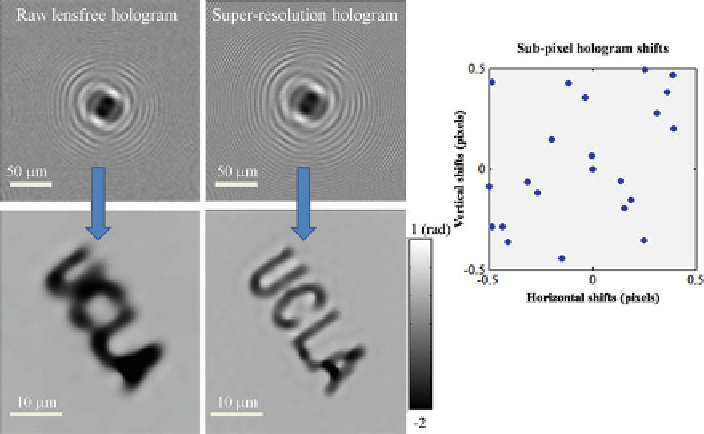
Fig. 4.10
A single raw lensfree hologram is compared against a super-resolved hologram, which
is the result of processing multiple raw and shifted holograms [
19
]. The sub-pixel shifts between
the different frames are shown on the
right
. The super-resolved hologram reveals more fringes and
resolves the aliasing apparent in the raw hologram. The additional fringes in the super-resolution
hologram translate to a higher spatial resolution image (after appropriate twin-image elimination
processing), as illustrated in the lower reconstructed images
After all the shifts of the lensfree raw holograms (each captured using an
individual LED within the source-array) are computed, the PSR algorithm can
be invoked. The goal of PSR is to find a single high-resolution hologram, which
recovers all the shifted low-resolution holograms once downsampled with the
appropriate shifts. A simple way to reach this desired hologram is to minimize the
following cost function:
Y
fl
Y
fl
;
X
1
2
˛
2
x
k;i
/
2
C.Y/
D
.x
k;i
Q
C
(4.3)
k
D
1;:::;p
i
D
1;:::;M
Q
where x
k
are the measured holograms,
x
k
are the corresponding images which are
obtained from downsampling the high-resolution image Y , and the index iruns
over all pixels of a given hologram. The last term in Eq.
4.3
penalizes very high-
frequency components which could be artifacts of the optimization process, and the
strength of this penalty can be adjusted using the parameter ˛. The cost function of
Eq.
4.3
is a quadratic function of the pixels of the high-resolution images and can
therefore be straightforwardly minimized using, for example, the conjugate gradient
descent method.
An experimental demonstration of the resolution enhancement due to the mul-
tiframe PSR is shown in Fig.
4.10
. A single raw low-resolution hologram and its