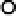Graphics Reference
In-Depth Information
Scanner
X
j
-
X
j
X
j
+
Figure 8.38.
3D sample points (black dots) and normal constraints (gray dots) for constructing
an interpolating implicit function.
points as samples at which
f
0. We want to extract a “reasonable” interpolating
3D surface that passes through these points. We must provide additional constraints
to prevent
f
(
X
j
)
=
0 for all
X
from being a viable solution; these come in the form of
normal constraints, as illustrated in Figure
8.38
. For example, we can travel a short
distance along the estimated normal in both directions at each point, generating a
point in front of the surface
X
j
(
X
)
=
and a point behind the surface
X
j
. Then we assign
X
j
X
j
points where the function
f
is constrained — either by an original range sample or
by a normal constraint — as
the values
f
(
)
=−
1 and
f
(
)
=
.
Similarly to Section
5.2.1
, we postulate a functional form for
f
that's a combination
of an affine term and a sum of radial basis functions centered at each point where we
have constrained its value:
{
X
j
,
j
=
1,
...
,
N
}
N
a
X
f
(
X
)
=
w
j
φ(
r
j
)
+
+
b
(8.22)
j
=
1
, and
r
j
=
X
X
j
2
. In 3D applications, we use the function
3
,
b
where
a
∈ R
∈ R
−
r
3
, both of which produce a smooth interpolation of the data. The
weights on the basis functions and the affine coefficients can be computed by solving
a linear system:
φ(
r
)
=
r
or
φ(
r
)
=
X
1
0
φ(
r
12
)
···
φ(
r
1
N
)
1
w
1
w
2
.
w
N
a
b
f
(
X
1
)
X
2
φ(
r
21
)
0
···
φ(
r
2
N
)
1
f
(
X
2
)
.
.
.
.
.
.
.
.
.
=
(8.23)
X
N
φ(
r
N
1
)φ(
r
N
2
)
···
(
X
N
)
0
0
0
1
f
X
1
X
2
···
X
N
00
1
1
···
1 00
21
In practice, we may not need to provide two normal constraints for every range point, especially if
the normal estimate is not reliable at the point.