Graphics Reference
In-Depth Information
degrees of freedom are relatively harmless; for example, six of them account for an
arbitrary rigid motion of the world coordinate system (which can be removed by
fixing the coordinate systemof the first camera as in Equation (
6.27
)). Another degree
of freedom corresponds to an unknown scale factor of the world; for example, an
image of a given object will look exactly the same as an image of an object that is
twice as large and twice as far away. This uncertainty can be resolved if we know the
physical length of some line segment in the scene that appears in one of the images
(e.g., the height of a table or wall).
However, the class of 3D projective transformations also includes generaliza-
tions of the shear and nonlinear distortions corresponding to the last two images
in Figure
5.1
. These distortions can have a serious effect on the structure of the scene
general 3D projective transformation can make the underlying true structure almost
unrecognizable, since angles and ratios of lengths are no longer preserved.
Without any further information about the cameras or the environment, this is
the best we can do for determining the camera matrices from feature matches in a
single image pair. A useful general formula for two camera matrices consistent with
a given
F
is
P
=[[
e
]
×
F
e
v
|
λ
e
]
P
=[
I
3
×
3
|
0
3
×
1
]
+
(6.31)
where
v
is any 3
is any nonzero scalar. This form shows that if we fix
P
to the canonical form in Equation (
6.31
), 4 degrees of projective ambiguity remain.
Beardsley et al. [
34
] recommended choosing
v
so that the left-hand matrix
×
1 vector and
λ
e
]
×
F
+
e
v
is as close to a rotation matrix as possible, resulting in a “quasi-Euclidean”
reconstruction.
[
(a)
(b)
(c)
(d)
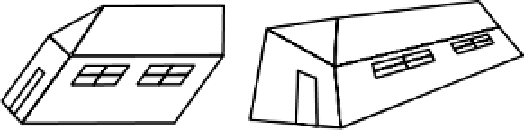
Figure 6.8.
Projective ambiguities inherent in the calibration of a stereo rig from featurematches
alone. These four scene configurations all differ by a 3D projective transformation and hence
can all produce the same image pair. (b) is a similarity transformation (rotation, translation,
and scale) of (a), (c) is a 3D shear, and (d) is a general 3D projective transformation. With-
out further information about the cameras or the environment, there is no way to resolve the
ambiguity.
13
Again, we can apply a counting argument: eleven degrees of freedom in each camera matrix
(allowing for nonzero skew) minus seven degrees of freedom for the fundamental matrix leaves
fifteen degrees of freedom in the 3D projective transformation
H
.