Digital Signal Processing Reference
In-Depth Information
N
i
M
! PfX ¼ x
i
g;
as
M>>
1
(2.218)
In this way, (
2.214
) becomes independent of the experiment and becomes the
characteristic of the random variable
X
, called the
mean
,or
expected
,
value
of the
random variable,
E
{
X
}.
m
emp
! EfXg;
as
M>>
1
(2.219)
From (
2.214
), (
2.218
), and (
2.219
), we have:
EfXg¼
X
N
x
i
PfX ¼x
i
g:
(2.220)
i¼
1
Other denotations used in literature are:
m
,
X
, and
hXi
. These denotations will
also be used throughout this text. When one would like to emphasize that
m
is the
mean value of the random variable
X
, one write
m
X
rather than
m
.
The next examples show that
E
{
X
} should not be interpreted as a value that we
would “expect”
X
to take.
Example 2.7.2
Find the mean value of the random variable
X
using only two
values:
x
1
¼
1 and
x
2
¼
0 where
P
{
x
1
}
¼ P
{
x
2
}
¼
0.5.
Solution
From (
2.220
), we have:
EfXg¼
1
0
:
5
þ
0
0
:
5
¼
0
:
5
:
(2.221)
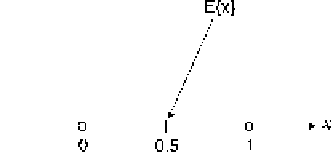
If
X
can only take the values 0 or 1, then we can never expect
X
to take the value
0.5 (see Fig.
2.38
).
Example 2.7.3
Consider a random variable with six values: 1, 2, 3, 4, 5, and 6, where
all six values of the random variable have the same probability (i.e.,
P
{
x
i
}
¼
1/6,
i ¼
1,
, 6). The mean value is:
...
EfXg¼
1
1
=
6
þ
2
1
=
6
þ
3
1
=
6
þ
4
1
=
6
þ
5
1
=
6
þ
6
1
=
6
¼
3
:
5
:
(2.222)
Fig. 2.38
Illustration of Example 2.7.2

Search WWH ::

Custom Search